实现优先队列
优先队列的一个最普遍的应用就是计算机在进行任务调度时,动态选择优先级最高的任务执行。即完成了一个操作后,后面的操作并不一定按照之前的优先级顺序执行,有可能会有其他优先级更高的任务插入,或者出现更加复杂的情况。在其他领域,只要涉及动态选择优先级顺序的情况,都需要用到优先队列。
当然优先队列不只有利于解决动态问题,解决一些静态问题也有优势。比如取出N各元素中的前M个元素。如果使用排序,其时间复杂度为O(NlogN),但是如果使用优先队列的话,其时间复杂度为O(NlogM).
优先队列有两个主要操作:入队和出队(取出优先级最高的元素).
| 数据结构 | 插入元素(入队) | 删除最大元素(出队) |
|---|---|---|
| 普通数组 | O(1) | O(n) |
| 顺序数组 | O(n) | O(1) |
| 堆 | O(logn) | O(logn) |
使用堆实现优先队列时,对于总共N个请求: 使用普通数组或者顺序数组,最差的情况:O(n^2),使用堆:O(nlogn)
优先队列一般都是基于堆的,所以先写堆的实现。
堆
详情可以看 堆和堆排序 中堆的算法部分.
- 堆中某个节点的值总是不大于或不小于其父节点的值(所以分为最大堆和最小堆)
- 堆总是一棵完全二叉树
另外要注意:节点值的大小和节点所处的层次是没有关系的
本文以最大堆为例,进行书写。
堆的表示方法——动态数组
堆的一种底层表示方法是使用动态数组实现,关于动态数组的实现见:https://homxuwang.github.io/2018/07/17/%E6%95%B0%E7%BB%84/
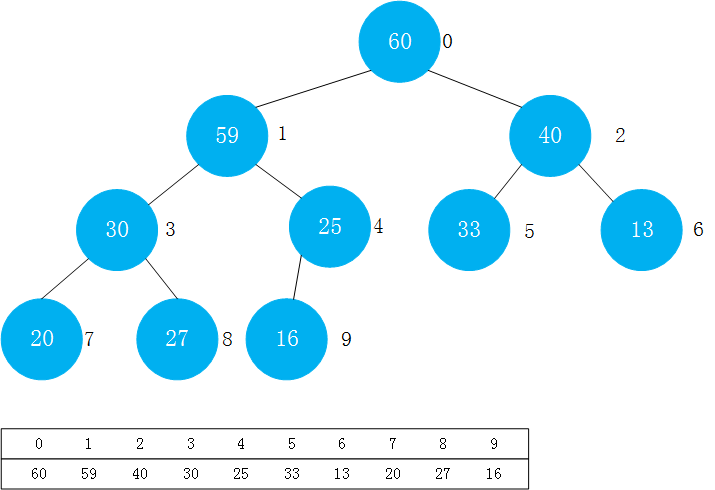
堆的实现代码:
public class MaxHeap<E extends Comparable<E>> {
private Array<E> data;
public MaxHeap(int capacity){
data = new Array<>(capacity);
}
public MaxHeap(){
data = new Array<>();
}
//返回堆中的元素个数
public int size() {
return data.getSize();
}
//判断堆是否为空
public boolean isEmpty() {
return data.isEmpty();
}
//返回一个完全二叉树的数组表示中,一个索引所表示的元素的父亲节点的索引
private int parent(int index){
if(index == 0)
throw new IllegalArgumentException("index 0 doesn't have parent;");
return (index-1) / 2;
}
//返回一个完全二叉树的数组表示中,一个索引所表示的元素的左孩子的索引
private int leftChild(int index){
return index * 2 + 1;
}
//返回一个完全二叉树的数组表示中,一个索引所表示的元素的右孩子的索引
private int rightChild(int index){
return index * 2 + 2;
}
//向堆中添加一个元素
public void add(E e){
data.addLast(e); //先向末尾添加元素
//调用siftUp函数,进行上浮操作,以维护堆的性质
siftUp(data.getSize() - 1);
}
//需要上浮的元素的索引
private void siftUp(int k){
//如果k满足索引大于零,且其父亲节点的值小于它的值,则进行上浮操作
while (k > 0 && data.get(parent(k)).compareTo(data.get(k)) < 0){
swap(k,parent(k));
k = parent(k);
}
}
//定义一个交换的函数
private void swap(int i , int j){
if(i < 0 || i >= data.getSize() || j < 0 || j>= data.getSize()){
throw new IllegalArgumentException("Index is illegal.");
}
E temp = data.get(i);
data.set(i,data.get(j));
data.set(j,temp);
}
//查看堆中的最大元素
public E findMax(){
if(data.getSize() == 0)
throw new IllegalArgumentException("Can not findMac in a empty heap");
return data.get(0);
}
//取出堆中的最大元素
public E extractMax(){
E ret = findMax();
swap(0,data.getSize() - 1);
data.removeLast();
siftDown(0);
return ret;
}
//下沉操作
private void siftDown(int k){
while (leftChild(k) < data.getSize()){//如果k没有左右孩子,则循环终止
int j = leftChild(k);//j为k的左孩子的索引
if(j + 1 < data.getSize() && data.get( j + 1 ).compareTo(data.get(j)) > 0){//如果k有右孩子,并且右孩子的节点的值大于左孩子的节点的值
j = rightChild(k);
//此时,data[j]是leftChild和rightChild中的最大值
}
if(data.get(k).compareTo(data.get(j)) >= 0) // 如果k的值大于其左右孩子的值,则满足了最大堆的另一个性质,可以退出循环体
break;
//否则交换k和j位置,并且k赋值为j,继续进行下一个循环
swap(k,j);
k = j;
}
}
}
- 在数组中,一个父亲节点其所有节点的索引(假设索引以0开始)为:
Index_leftChild = index_Father * 2 + 1; Index_rightChild = index_Father * 2 + 2; - 如果知道一个孩子节点的索引(假设索引以0开始)求其父亲节点的索引:
index_Father = ( index_Child - 1 ) / 2;上面两个求法可以用数学归纳法进行证明。
-
Sift Up操作很简单,即新添加的元素先放到数组的末尾位置,这时候满足了完全二叉树的性质。但是它不一定满足总是不大于或者不小于其父亲节点的值。所以这时候的操作是,这个值要与它的父亲节点、爷爷节点……对比,直到放在合适的位置。因为方法中总结了找到一个节点的父亲节点的方法:faterIndex = (index-1) / 2。以一个最大堆为例,让新加入的节点和父亲节点对比,如果它大于其父亲节点,则交换,继续对比其父亲节点,直到它小于等于其父亲节点为止。 Sift Down操作,即取出最大堆的堆顶的元素(取出操作只能取出这个最大的元素,而不能取出别的元素)。因为最大的元素取出后,其左右的树结构就是两个单独的子树,那么要给这两个子树找一个新的父节点,操作如下:- 将堆中的最后一个元素放在堆顶
- 删除掉最后一个元素(这时候满足完全二叉树的性质)
- 将堆顶元素与左右孩子中
大于它且较大的数进行交换 - 交换后的新位置继续与孩子节点中
大于它且较大的数进行交换 - 继续操作直到它大于其左后孩子或者它没有左右孩子
优点:add操作和extractMax操作的时间复杂度都是O(logn)
- 其中
swap交换函数我写在了堆这个类中,可以在Array类中定义交换函数,在堆类中直接调用即可。
Heapify 和 replace操作
replace
replace:取出最大元素后放入新元素
- step1: extractMax -> step2: add (2O(logn))
- setp1: 替换堆顶元素 -> step2: Sift Down (O(logn))
//取出堆中的最大元素,并替换成e public E replace(E e){ E ret = findMax(); data.set(0,e); siftDown(0); return ret; }Heapify
将任意数组整理成堆的形状
- 扫描数组,放如堆的新的对象中再返回 (O(nlogn))
- 可以先把数组看成一棵完全二叉树,从最后一个非叶子节点开始进行
Sift Down操作。(找到最后一个非叶子节点的方法:拿到最后一个节点的索引,然后计算他的父亲节点的索引即可) step1: 找到最后一个非叶子节点,进行Sift Down操作 step2: 倒数第二个非叶子节点进行Sift Down操作 … 以此类推 直到索引为0的非叶子节点完成Sift Down操作 O(n) - Heapify一般可以在构造函数中进行(用一个数组初始化堆)),所以Array类也要支持一个用数组初始化动态数组的构造函数
Array类的构造函数:
public Array(E[] arr) {
data = (E[])new Object[arr.length];
for(int i = 0 ; i < arr.length ; i ++){
data[i] = arr[i];
}
size = arr.length;
}
MaxHeap的构造函数:
public MaxHeap(E[] arr){
data = new Array<>(arr);
for(int i = parent(arr.length - 1) ; i >= 0 ; i--)
siftDown(i);
}
优先队列
优先队列就是一个队列,要满足队列的所有属性方法,所以要实现队列接口,关于队列的实现见:https://homxuwang.github.io/2018/07/17/%E5%AE%9E%E7%8E%B0%E6%A0%88%E5%92%8C%E9%98%9F%E5%88%97/
优先队列的底层是使用堆来实现,同样还是以最大堆为例。
public class PriorityQueue<E extends Comparable<E>> implements Queue<E> {
private MaxHeap<E> maxHeap;
public PriorityQueue(){
maxHeap = new MaxHeap<>();
}
@Override
public int getSize() {
return maxHeap.size();
}
@Override
public boolean isEmpty() {
return maxHeap.isEmpty();
}
@Override
public void enqueue(E e) {
maxHeap.add(e);
}
@Override
public E dequeue() {
return maxHeap.extractMax();
}
@Override
public E getFront() {
return maxHeap.findMax();
}
}
- java.util中的PriorityQueue默认是用的最小堆,具体方法名也有一些区别