实现栈和队列
栈
栈在计算机中有很广泛的应用,比如括号的匹配用到了栈,系统栈,撤销操作。
栈也是一种线性结构。相比数组,栈对应的操作是数组的子集。只能从一端添加元素,从同一端取出元素,即栈顶。是一种后进先出的数据结构(Last In First Out (LIFO))
栈的实现
栈的实际底层实现有多种方式,如动态数组,链表等。
这里只实现栈的几个基本操作:入栈,出栈,查看栈顶元素,查看栈元素数量,查看栈是否为空。
定义Stack接口,基于动态数组实现栈,动态数组的实现见
https://homxuwang.github.io/2018/07/17/%E6%95%B0%E7%BB%84/
首先在程序中创建上面链接中的Array类 然后创建Stack接口 Interface Stack<E>
public interface Stack<E> {
int getSize(); //获取元素个数
boolean isEmpty(); //判断是否为空
void push(E e); //进栈
E pop(); //出栈
E peek(); //查看栈顶元素
}
ArrayStack基于动态数组实现的栈类
public class ArrayStack<E> implements Stack<E> {
Array<E> array;
/**
* 构造函数
* @param capacity 定义容量
*/
public ArrayStack(int capacity){
array = new Array<>(capacity);
}
/**
* 无参构造函数
*/
public ArrayStack(){
array = new Array<>();
}
@Override
public int getSize(){
return array.getSize();
}
@Override
public boolean isEmpty() {
return array.isEmpty();
}
//获得栈的容量,这个方法与栈的接口无关,只有在使用动态数组的时候才有这个方法
public int getCapacity(){
return array.getCapacity();
}
@Override
public void push(E e){
array.addLast(e);
}
@Override
public E pop(){
return array.removeLast();
}
@Override
public E peek(){
return array.getLast();
}
@Override
public String toString(){
StringBuilder res = new StringBuilder();
res.append("Stack:");
res.append("[");
for(int i = 0 ; i < array.getSize(); i++){
res.append(array.get(i));
if(i != array.getSize() - 1){
res.append(",");
}
}
res.append("] top");
return res.toString();
}
}
在Main函数中进行测试:
public class Main {
public static void main(String[] args){
ArrayStack<Integer> stack = new ArrayStack<>();
for(int i = 0 ; i < 4 ; i++){
stack.push(i);
System.out.println(stack);
}
stack.pop();
System.out.println(stack);
}
}
结果如下: 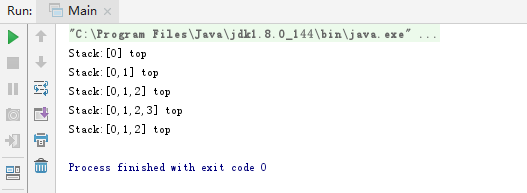
栈的复杂度分析
ArrayStack
void push(e) O(1) 均摊 E pop() O(1) 均摊 E peek() O(1) int getSize() O(1) boolean isEmpty() O(1)
队列
队列也是一种线性结构。先进先出(First In First Out(FIFO))
一般队列的实现
定义Queue接口,基于动态数组实现队里,动态数组的实现见
https://homxuwang.github.io/2018/07/17/%E6%95%B0%E7%BB%84/
基于Array类创建Queue接口
Interface Queue<E>
public interface Queue<E>{
int getSize(); //获取元素个数
boolean isEmpty; //判断队列是否为空
void enqueue(E e); //入队
E dequeue(); //出队
E getFront(); //查看队首元素
}
底层采用动态数组Array类来实现队列,创建队列类ArrayQueue:
public class ArrayQueue<E> implements Queue<E> {
private Array<E> array;
public ArrayQueue(int capacity){
array = new Array<>(capacity);
}
public ArrayQueue(){
array = new Array<>();
}
@Override
public int getSize(){
return array.getSize();
}
@Override
public boolean isEmpty(){
return array.isEmpty();
}
public int getCapacity(){
return array.getCapacity();
}
@Override
public void enqueue(E e){
array.addLast(e);
}
@Override
public E dequeue(){
return array.removeFirst();
}
@Override
public E getFront(){
return array.getFirst();
}
@Override
public String toString(){
StringBuilder res = new StringBuilder();
res.append("Queue:");
res.append("front[");
for(int i = 0 ; i < array.getSize() ; i ++){
res.append(array.get(i));
if(i != array.getSize() - 1)
res.append(",");
}
res.append("]end");
return res.toString();
}
}
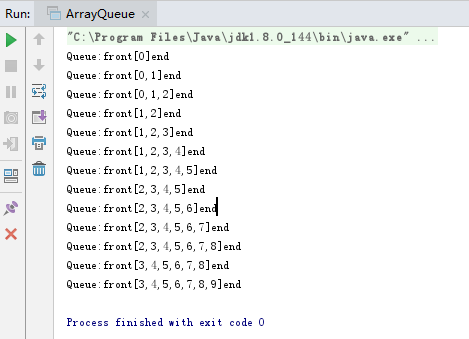
简单测试:
public static void main(String[] args){
ArrayQueue<Integer> queue = new ArrayQueue<>();
for(int i = 0 ; i < 10 ; i++){
queue.enqueue(i);
System.out.println(queue);
if(i % 3 == 2){
queue.dequeue();
System.out.println(queue);
}
}
}
一般队列的复杂度分析
void enqueue(E) O(1) 均摊 E dequeue() O(n) E getFront() O(1) int getSize() O(1) boolean isEmpty() O(1)
可以看到一般队列的出队过程因为要往前挪动一个元素,导致其时间复杂度是O(n)
循环队列的实现
在一般队列的基础上,引入front指向队列头,tail指向队列尾。front == tail 队列为空。在出队后,不用挪动元素,而是让front的指向后移,同时,添加元素时tail向后挪,指向第一个未添加元素的地方。在队列满的情况下,索引+1后对数组长度求余得到tail的位置。但是若tail指向的事最后一个未添加元素的位置时,再向其中添加元素,此时tail后挪后就导致tail == front而当front == tail时表示队列为空。所以用(tail + 1) % 数组容量 == front(tail + 1 % 数组容量 是因为如图,如果front == 0 ,tail == 7时也是满的) 表示队列已满,这时候进行扩容。即浪费一个空间。
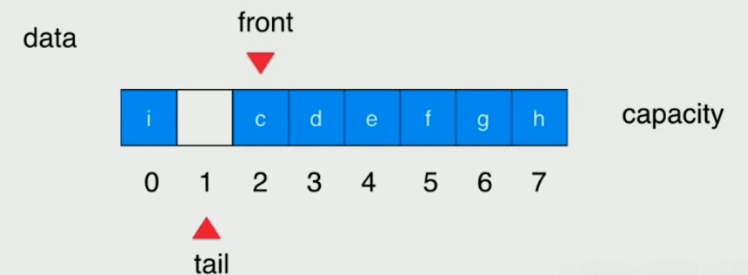
循环队列底层不再使用上文将到的动态数组
public class LoopQueue<E> implements Queue<E> {
private E[] data;
private int front, tail; //front表示队首所指的索引,tail指向队列最后一个元素的下一个位置所在的索引,也就是入队新的元素所存放的位置对应的索引
private int size; //队列中有多少元素(也可以用tail和front进行控制)
//构造函数
public LoopQueue(int capacity){
data = (E[])new Object[capacity + 1]; //因为上文提到要预留一个空间,所以这里+1
front = 0;
tail = 0;
size = 0;
}
//无参构造函数
public LoopQueue(){
this(10);
}
public int getCapacity(){
return data.length - 1; //真正能够存储的数据大小是length - 1,因为预留了一个空间
}
@Override
public boolean isEmpty(){
return front == tail;
}
@Override
public int getSize(){
return size;
}
@Override
public void enqueue(E e){
if((tail + 1) % data.length == front){ //如果队列满了,则调用resize()函数
resize(getCapacity() * 2);
}
data[tail] = e;
tail = (tail + 1) % data.length;
}
@Override
public E dequeue(){
if(isEmpty()){
throw new IllegalArgumentException("Canno dequeuq from an empty queue");
}
E temp = data[front];
data[front] = null;
front = (front + 1) % data.length;
size --;
if(size == getCapacity() / 4 && getCapacity() / 2 != 0){ //如果队列元素个数小于容量的1/4则进行缩容
resize(getCapacity() / 2);
}
return temp;
}
@Override
public E getFront(){
if(isEmpty()){
throw new IllegalArgumentException("Queue is empty");
}
return data[front];
}
private void resize(int newCapacity){
E[] newData = (E[])new Object[newCapacity + 1];
for(int i = 0 ; i < size ; i++){
newData[i] = data[(front + i) % data.length];
}
data = newData;
front = 0;
tail = size;
}
/**
*便于打印输出
*/
@Override
public String toString(){
StringBuilder res = new StringBuilder();
res.append(String.format("Queue: Size = %d , capacity = %d \n",size,getCapacity()));
res.append("front[");
for(int i = front ; i != tail ; i = (i + 1 ) % data.length){
res.append(data[i]);
if((i + 1) % data.length != tail)
res.append(", ");
}
res.append("] tail");
return res.toString();
}
}
测试代码:
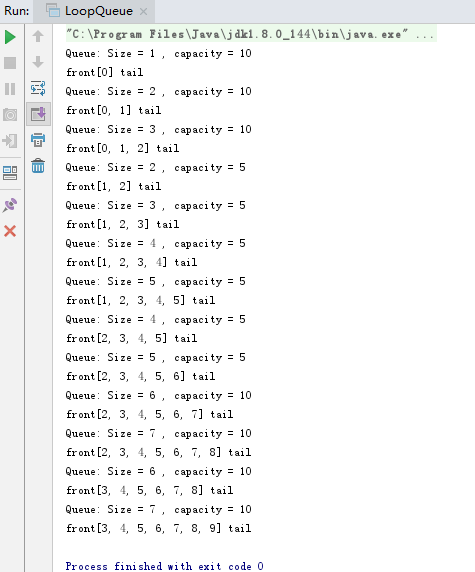
public static void main(String[] args){
LoopQueue<Integer> queue = new LoopQueue<>();
for(int i = 0 ; i < 10 ; i++){
queue.enqueue(i);
System.out.println(queue);
if(i % 3 == 2){
queue.dequeue();
System.out.println(queue);
}
}
}
代码结果: