实现线段树
定义
当更关心某个区间上的问题时,使用线段树(区间树)会更方便。
- 线段树是一种二叉搜索树
- 线段树每个节点存放一个区间内相应的信息
- 一般用静态数组表示
- 线段树不一定是一棵完全二叉树
- 线段树是平衡二叉树(最大深度和最小深度的差最大为1)
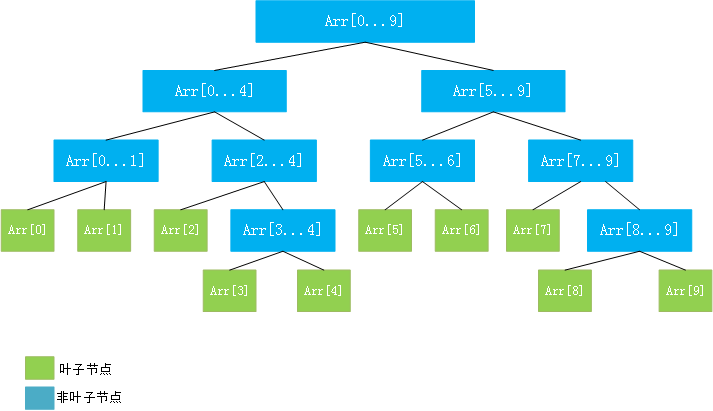
例如,如果线段树想表示区间的和,那么每个节点存放的不是对应的数组,而是这个区间的和。
线段树依然可以使用数组表示。 那么对于一个区间有n个元素,数组的大小该如何确定? 对于一个满二叉树,如果有h层(从0层到h-1层),那么h层就有2^h-1个节点,差不多是2^h,最后一层(h-1)层,有2^(h-1)个节点,最后一层的节点的数目大约是前面的几点数目之和。
所以,如果用数组开辟空间,那么如果n=2^k(即恰好为2的整数次幂),需要2n的空间(这是满二叉树的情况),但是如果n=2^k+1(即n>2^k,也就是最坏的情况),则需要4n的空间。
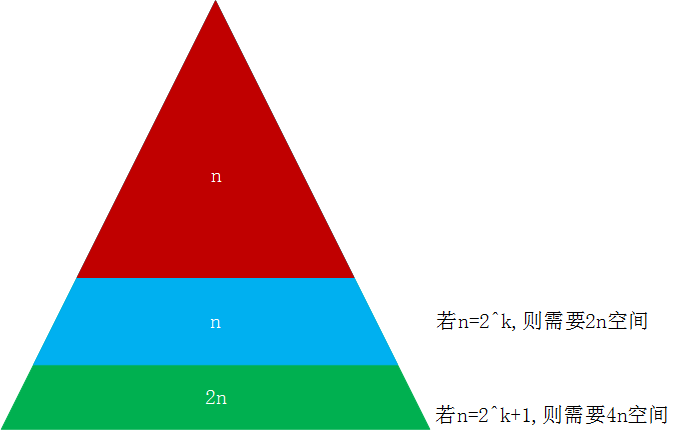
结论:因为线段树不考虑添加元素,也就是区间的大小是固定的,所以使用4n的静态空间就可以满足所有情况。(这里有空间浪费)
创建线段树
线段树的根节点的信息,是两个孩子节点的信息的综合。比如求和,根节点的值就是左右孩子节点的值之和,依次类推,那么可以采用递归的方法进行求值。
另外,在进行线段树的创建时,因为不知道要采取什么样的方法去创建(比如求和,求积,求最大值,求最小值等),所以可以定义一个Merger接口,要求在创建线段树时,其构造函数不但要传入一个初始的数组,也要传入一个merger,即相应的要采取的操作。
Merger:
//融合器,即线段树进行什么操作(求和或者求乘积等操作)
public interface Merger<E> {
E merge(E a,E b);
}
public class SegmentTree<E> {
private E[] data;//数组arr的副本
private E[] tree; // 将数据以树的形式表示出来,看成一个满二叉树
private Merger<E> merger; //传入一个merger,定义用户要进行的操作
public SegmentTree(E[] arr,Merger<E> merger){
this.merger = merger;
data = (E[]) new Object[arr.length];
for(int i = 0 ; i < arr.length ; i++){
data[i] = arr[i];
}
tree = (E[]) new Object[4 * arr.length];
buildSegmentTree(0,0,data.length - 1 );//创建SegmentTree
}
public int getSize(){
return data.length;
}
public E get(int index){
if(index < 0 || index >= data.length)
throw new IllegalArgumentException("Index is illegal.");
return data[index];
}
//返回以完全二叉树的数组表示中,一个索引表示的元素的左孩子所在节点的索引
private int leftChild(int index){
return index * 2 + 1;
}
//返回以完全二叉树的数组表示中,一个索引表示的元素的右孩子所在节点的索引
private int rightChild(int index){
return index * 2 + 2;
}
/**
*在treeIndex的位置创建表示区间[l,r]的线段树
* @param treeIndex 要创建的线段树根节点对应的索引
* @param l 对于此节点对应的左端点
* @param r 对于此节点对应的右端点
*/
private void buildSegmentTree(int treeIndex,int l , int r){
if(l == r){
tree[treeIndex] = data[l];
return;
}
//l < r
//左右子树的index,即在数组中的索引
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
//左右子树相应的区间的中间位置
int mid = l + (r - l) / 2; //为了防止(l + r) / 2 溢出
buildSegmentTree(leftTreeIndex,l,mid);
buildSegmentTree(rightTreeIndex,mid+1,r);
//调用merger接口类对象,进行相应的操作
tree[treeIndex] = merger.merge(tree[leftTreeIndex],tree[rightTreeIndex]);
}
@Override
public String toString(){
StringBuilder res = new StringBuilder();
res.append('[');
for(int i = 0 ;i < tree.length ; i++){
if(tree[i] != null)
res.append(tree[i]);
else
res.append("null");
if(i != tree.length - 1)
res.append(",");
}
res.append(']');
return res.toString();
}
}
在Main函数中进行测试,并打印结果:
public class Main {
public static void main(String[] args){
Integer[] nums = {-2,0,3,-5,2,-1};
SegmentTree<Integer> segTree = new SegmentTree<>(nums, new Merger<Integer>() {
@Override
public Integer merge(Integer a, Integer b) {
return a + b;
}
});
System.out.println(segTree);
}
}

生成如下的线段树: 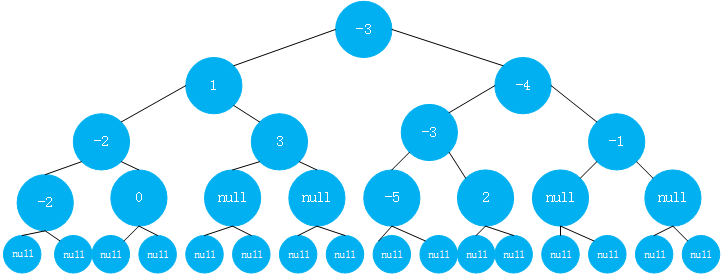
线段树的查询操作
用户可以输入要查询的某个区间,返回这个区间内的对应的值。
相应的方法:
/*
返回要查询的区间[queryStart,queryEnd]的值
*/
public E query(int queryStart,int queryEnd){
if(queryStart < 0 || queryStart >= data.length || queryEnd < 0 || queryEnd >= data.length || queryStart > queryEnd)
throw new IllegalArgumentException("Illegal Index");
return query(0,0,data.length-1,queryStart,queryEnd);
}
/**
* 定义私有函数,在以treeIndex为根的线段树中[l,r]的范围里,搜索区间[queryStart,queryEnd]的值
* @param treeIndex 要查询的树的根节点
* @param l 树对应的数组的左范围
* @param r 树对应的数组的右范围
* @param queryStart 要查询的区间的左端
* @param queryEnd 要查询的区间的右端
*/
private E query(int treeIndex,int l,int r,int queryStart,int queryEnd){
if(l == queryStart && r == queryEnd)
return tree[treeIndex];
int mid = l + (r - l) / 2;
int leftIndex = leftChild(treeIndex);
int rightIndex = rightChild(treeIndex);
if(queryStart >= mid+1)
return query(rightIndex,mid+1,r,queryStart,queryEnd);
else if(queryEnd <= mid)
return query(leftIndex,l,mid,queryStart,queryEnd);
//否则,跨左右区间,分别求左右区间的值,然后merg,返回
E leftResult = query(leftIndex,l,mid,queryStart,mid);
E rightResult = query(rightIndex,mid+1,r,mid+1,queryEnd);
return merger.merge(leftResult,rightResult);
}
线段树的更新操作
线段树的更新,是针对某个index位置的数据进行更新,使用线段树进行更新操作,其时间有优势,时间复杂度为O(logn)
更新操作的代码如下:
/**
* 将index位置的值更新为e
* @param index 待更新的位置索引
* @param e 更新后的值
*/
public void set(int index,E e){
if(index < 0 || index >= data.length)
throw new IllegalArgumentException("Illegal index.");
set(0,0,data.length - 1,index,e);
}
//在以treeIndex为根的线段树中,更新index的值为e
private void set(int treeIndex,int l , int r,int index,E e){
if(l == r){
tree[treeIndex] = e;
return;
}
int mid = l +(r - l) / 2;
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
if(index >= mid+1)
set(rightTreeIndex,mid+1,r,index,e);
else //index <= mid
set(leftTreeIndex,l,mid,index,e);
tree[treeIndex] = merger.merge(tree[leftTreeIndex],tree[rightTreeIndex]);
}