排序算法
最近在学习数据结构和算法,这里总结一下学习的排序算法。
选择排序 - SelectionSort
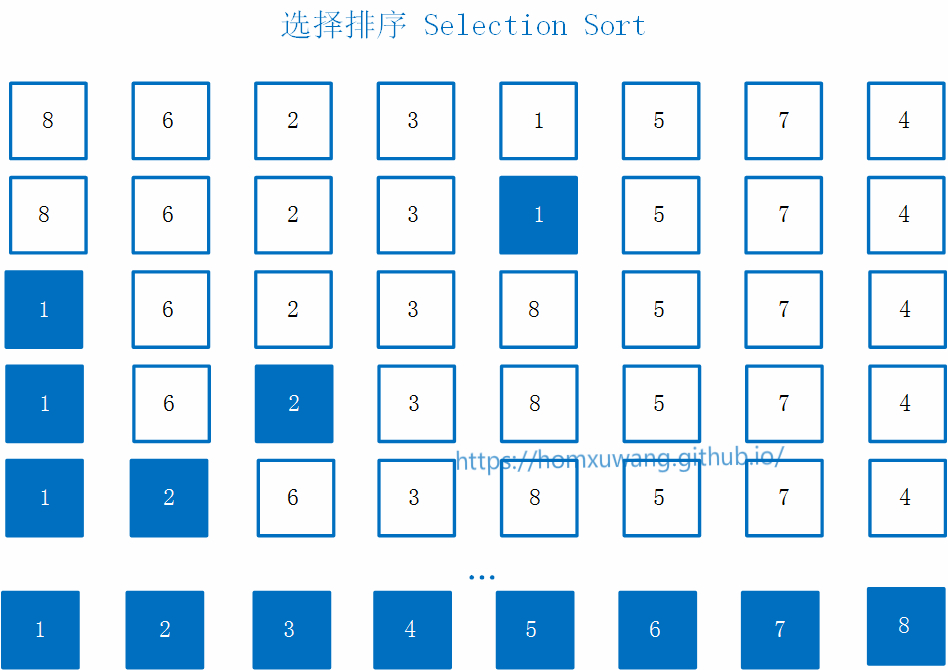
基本思路: 假设有一个数组(如图所示),进行从小到大的排序。首先在整个数组范围里,找出要放在第一个位置的数,也就是最小的数:1,然后将1和现在的第一名的位置8进行换位,经过交换以后,1所处的位置就是最终排序所在的位置,这样就继续在剩下的部分找此时最小的数,也就是2,然后把2和相应的第二个位置所在的元素进行交换,此时1和2两个元素也已经是最终排好序的结果。整个过程以此类推,继续在剩下的部分中找此时最小的元素,然后进行交换位置。。。。。
代码实现:
public class SelectionSort {
// 算法类不允许产生任何实例
private SelectionSort(){}
public static void sort(int[] arr){
int n = arr.length;
for( int i = 0 ; i < n ; i ++ ){
// 寻找[i, n)区间里的最小值的索引
int minIndex = i;
for( int j = i + 1 ; j < n ; j ++ )
if( arr[j] < arr[minIndex] )
minIndex = j;
swap( arr , i , minIndex);
}
}
private static void swap(int[] arr, int i, int j) {
int t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
public static void main(String[] args) {
int[] arr = {10,9,8,7,6,5,4,3,2,1};
SelectionSort.sort(arr);
for( int i = 0 ; i < arr.length ; i ++ ){
System.out.print(arr[i]);
System.out.print(' ');
}
System.out.println();
}
}
改进:
import java.util.*;
public class SelectionSort{
// 算法类不允许产生任何实例
private SelectionSort(){}
public static void sort(Comparable[] arr){
int n = arr.length;
for( int i = 0 ; i < n ; i ++ ){
// 寻找[i, n)区间里的最小值的索引
int minIndex = i;
for( int j = i + 1 ; j < n ; j ++ )
// 使用compareTo方法比较两个Comparable对象的大小
if( arr[j].compareTo( arr[minIndex] ) < 0 )
minIndex = j;
swap( arr , i , minIndex);
}
}
private static void swap(Object[] arr, int i, int j) {
Object t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
}
插入排序 - InsertionSort
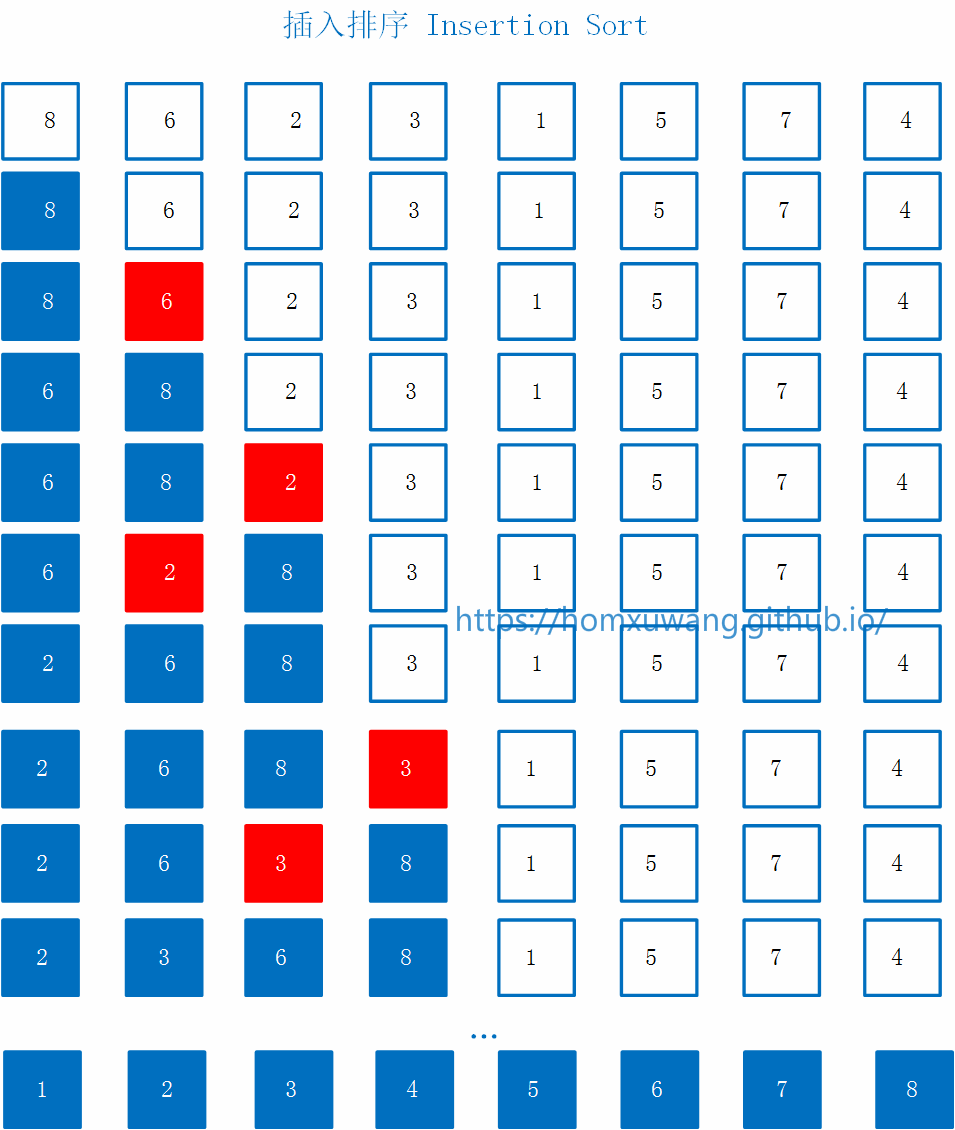
基本思路: 开始只考虑8这个元素的时候,它就已经排好序了。 接着看6这个元素,接下来的步骤是把6与它前面的数组进行比较,放在合适的位置,当6与8比较时,6<8,所以6在8前面位置。 接着看2这个元素,2与它前面的数组进行比较,2<8,所以2和8交换一次位置,2继续和6比较,2<6,所以2和6交换位置,此时2在最前面的位置。 接着看3这个元素,3比8小,所以交换一次位置,3又比6小,所以交换一次位置,3比2大所以不进行交换操作,3插入在2和6中间,这时前面的4个元素排序完成。 以此类推。
代码实现:
import java.util.*;
public class InsertionSort{
private InsertionSort(){}
public static void sort(Comparable[] arr){
int n = arr.length;
for (int i = 0; i < n; i++) {
// 寻找元素arr[i]合适的插入位置
// 写法1
// for( int j = i ; j > 0 ; j -- )
// if( arr[j].compareTo( arr[j-1] ) < 0 )
// swap( arr, j , j-1 );
// else
// break;
// 写法2
for( int j = i; j > 0 && arr[j].compareTo(arr[j-1]) < 0 ; j--)
swap(arr, j, j-1);
}
}
private static void swap(Object[] arr, int i, int j) {
Object t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
}
插入排序和选择排序相比,如果满足了条件就有机会提前结束,所以它的排序效率理论上要比选择排序高 但是实际上它的运行时间比选择排序要慢,这是因为其swap操作较多,浪费了时间,所以针对这个地方进行改进
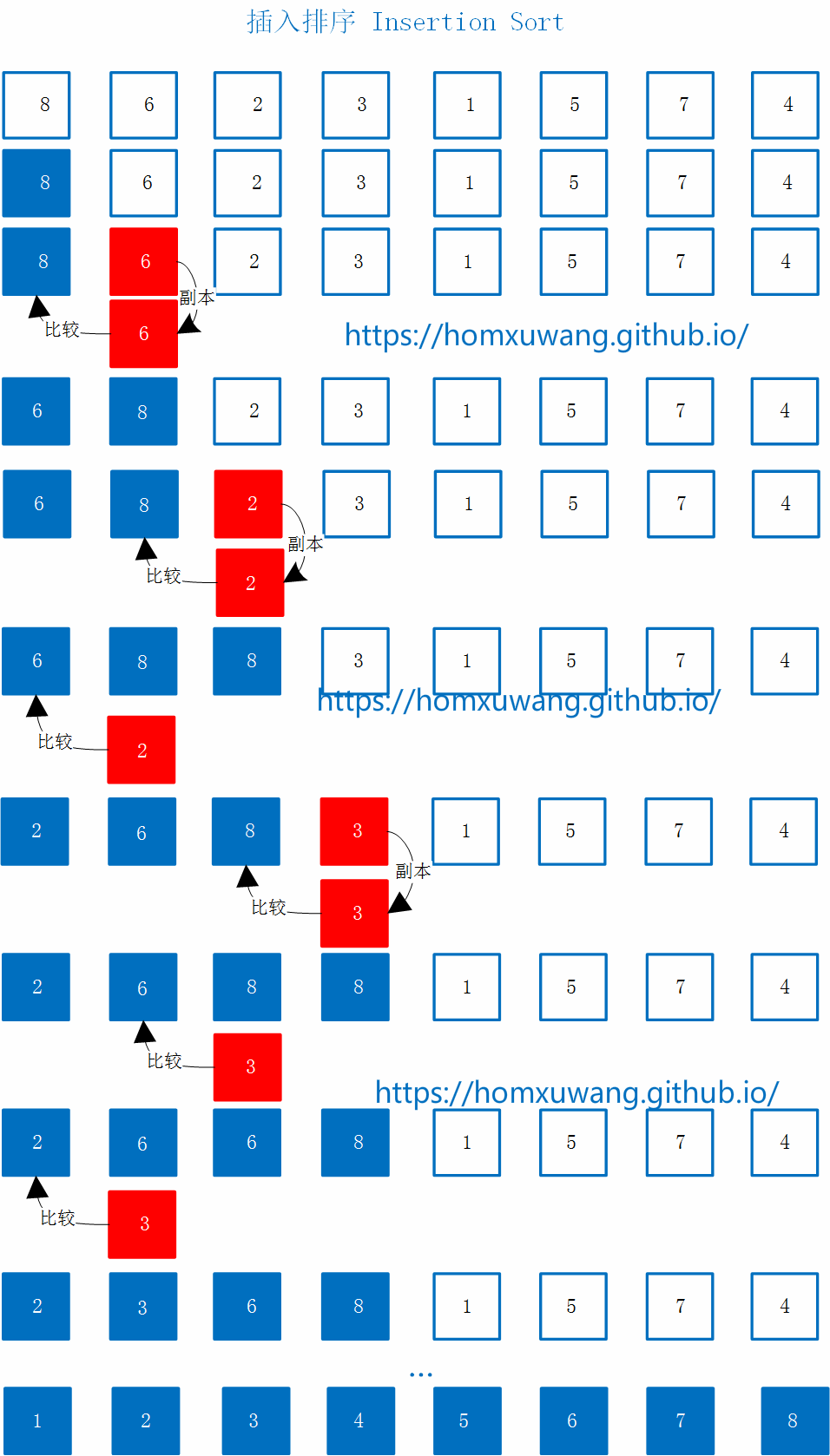
改进代码思路: 首先,对位置0处的元素不作处理。
接着,看位置1处的元素6,首先对元素6做一个副本保存起来,然后看元素6是否应该在当前位置,即让他与前面的元素进行对比,如果小于前面的元素,则当前元素位置的值赋值为前一个元素的值,前一个元素位置的值赋值为刚才保存起来的副本(即当前元素的值)。(其实这也是相当于一个交换操作,在满足前一个元素大于当前元素值的情况下,进行交换值操作)
接着,看位置2处的元素2,首先对元素2做一个副本保存起来,然后元素2与前一个元素8比较,2<8,则将元素2处的值赋值为8;接着再比较位置1处的元素8与位置1处的元素6的大小,将位置1处的值赋值为元素6,接着将元素2放在第一个位置。这样就少进行了交换的操作。
接着,看元素3,首先对元素3做一个副本保存起来,然后看元素3该不该放在当前位置,发现3<8,所以这个位置赋值为8;然后看3是不是该放在刚才元素8的位置,发现元素3比元素6小,所以元素6放在刚才元素8的位置;然后看元素3是不是该放在刚才元素6的位置,发现元素3比元素2大,所以元素3应该放在这个位置。
这样很多交换操作就通过赋值进行取代了,所以性能更好。
改进代码:
import java.util.*;
public class InsertionSort{
// 我们的算法类不允许产生任何实例
private InsertionSort(){}
public static void sort(Comparable[] arr){
int n = arr.length;
for (int i = 0; i < n; i++) {
// 寻找元素arr[i]合适的插入位置
// 写法1
// for( int j = i ; j > 0 ; j -- )
// if( arr[j].compareTo( arr[j-1] ) < 0 )
// swap( arr, j , j-1 );
// else
// break;
// 写法2
// for( int j = i; j > 0 && arr[j].compareTo(arr[j-1]) < 0 ; j--)
// swap(arr, j, j-1);
// 写法3
Comparable e = arr[i];
int j = i;
for( ; j > 0 && arr[j-1].compareTo(e) > 0 ; j--)
arr[j] = arr[j-1];
arr[j] = e;
}
}
private static void swap(Object[] arr, int i, int j) {
Object t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
}
归并排序 - MergeSort
自顶向下的归并排序
基本思路: 所谓归并排序,有两大步,一步是归,一步是并。
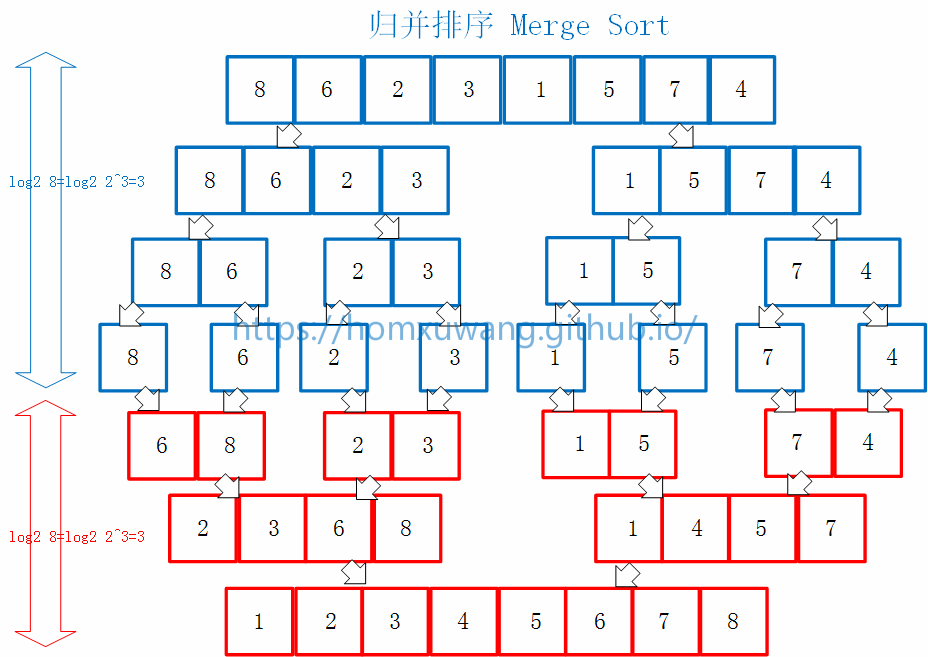
当对一个数组进行排序的时候,先把这个数组分成一半,然后分别把左边的数组和右边的数组排序,之后再归并起来。在对左边数组和右边的数组进行排序的时候,再次分别把左边的数组和右边的数组分成一半,然后对每一个部分进行排序。一样的,对这每一个部分进行排序的时候,再次把他们分成一半,直到它们只含有一个元素的时候,已经是有序了。(蓝色部分)
这时候就对上面最终分割完成的各个部分进行归并。在归并到上一个层级之后,继续进行归并,逐层上升,进行归并,直到归并到最后一层的时候,整个数组就有序了。(红色部分)
可以看到,对图中的8各元素进行归并的时候,分成3级,第三级就可以把数组分成单个元素了,这样每次二分,就是log2 8 = 3,如果是N个元素,则有log2 N的层级。每一层要处理的元素个数是一样的,则整个归并过程是N*log(N)的时间复杂度。
那么问题是假设左半部分和右半部分已经排好了序,怎么把他们合并成一个有序的数组。 这个过程需要为数组开辟一个相同大小的临时空间进行辅助,如下图。 在合并成一个数组的过程中,需要3个索引:k是最终在归并过程中要跟踪的位置,i和j分别表示两个排好序的数组,当前要考虑的元素项。 首先看1和2两个元素,谁应该放在k位置,进行对比后,较小的元素1放在k位置。这时候k++,j++。 紧接着,元素2和元素4进行对比,较小的元素2放在当前的k位置,这时候k++,i++。 继续元素3和元素4进行对比,较小的元素3放在当前的k位置,这时候k++,i++。 继续元素6和元素4进行对比,较小的元素4放在当前的k位置,这时候k++,j++。 。。。。 算法过程中,需要维护k,i,j满足算法的定义。并且需要跟踪i,j的越界情况。 这里定义l(left),r(right),和m(middle)分别为整个数组的最左边的元素,数组最右边的元素和中间位置的元素(这里指定为第一个数组的最后一个元素)。这里再做一个说明,这里的定义整个算法的数组是前闭后闭的数组。
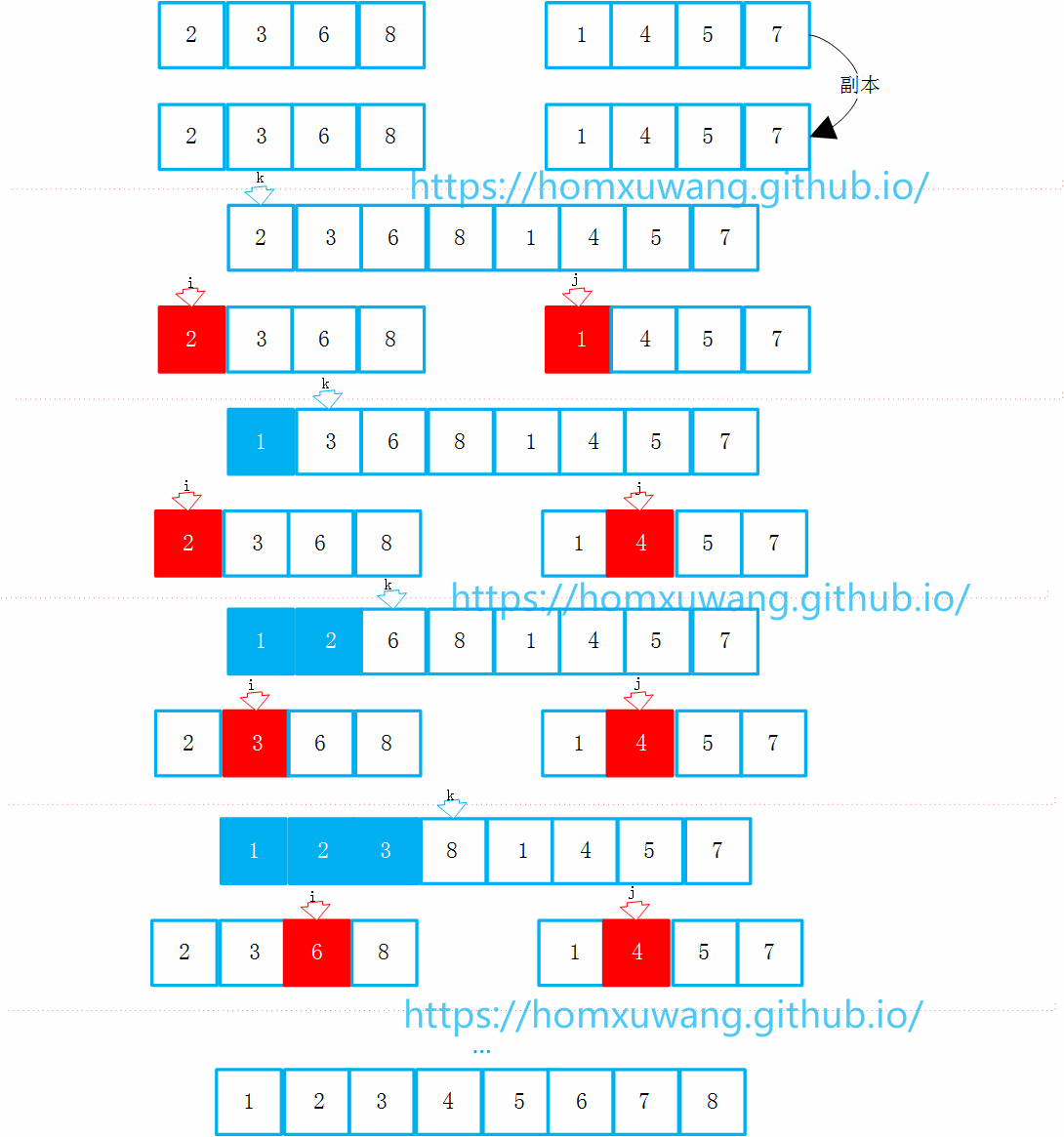
代码实现:
import java.util.*;
public class MergeSort{
// 我们的算法类不允许产生任何实例
private MergeSort(){}
// 将arr[l...mid]和arr[mid+1...r]两部分进行归并
private static void merge(Comparable[] arr, int l, int mid, int r) {
Comparable[] aux = Arrays.copyOfRange(arr, l, r+1);
// 初始化,i指向左半部分的起始索引位置l;j指向右半部分起始索引位置mid+1
int i = l, j = mid+1;
for( int k = l ; k <= r; k ++ ){
if( i > mid ){ // 如果左半部分元素已经全部处理完毕
arr[k] = aux[j-l]; j ++;
}
else if( j > r ){ // 如果右半部分元素已经全部处理完毕
arr[k] = aux[i-l]; i ++;
}
else if( aux[i-l].compareTo(aux[j-l]) < 0 ){ // 左半部分所指元素 < 右半部分所指元素
arr[k] = aux[i-l]; i ++;
}
else{ // 左半部分所指元素 >= 右半部分所指元素
arr[k] = aux[j-l]; j ++;
}
}
}
// 递归使用归并排序,对arr[l...r]的范围进行排序
private static void sort(Comparable[] arr, int l, int r) {
if (l >= r)
return;
int mid = (l+r)/2;
sort(arr, l, mid);
sort(arr, mid + 1, r);
merge(arr, l, mid, r);
}
public static void sort(Comparable[] arr){
int n = arr.length;
sort(arr, 0, n-1);
}
}
自底向上的归并排序
基本思路: 自底向上的归并排序的基本原理是,给定一个数组,从左向右将数组依次划分为小段,如两个元素一个小段,然后进行归并排序。当这一轮归并排序完成之后,再四个元素一个小段进行归并排序,最后八个元素一个小段进行归并排序。以上面的数组为例,这时候就排序完成了。 这种方法并不需要递归,只需要迭代就可以完成排序操作。
代码实现:
import java.util.*;
public class MergeSortBU{
// 我们的算法类不允许产生任何实例
private MergeSortBU(){}
// 将arr[l...mid]和arr[mid+1...r]两部分进行归并
private static void merge(Comparable[] arr, int l, int mid, int r) {
Comparable[] aux = Arrays.copyOfRange(arr, l, r+1);
// 初始化,i指向左半部分的起始索引位置l;j指向右半部分起始索引位置mid+1
int i = l, j = mid+1;
for( int k = l ; k <= r; k ++ ){
if( i > mid ){ // 如果左半部分元素已经全部处理完毕
arr[k] = aux[j-l]; j ++;
}
else if( j > r ){ // 如果右半部分元素已经全部处理完毕
arr[k] = aux[i-l]; i ++;
}
else if( aux[i-l].compareTo(aux[j-l]) < 0 ){ // 左半部分所指元素 < 右半部分所指元素
arr[k] = aux[i-l]; i ++;
}
else{ // 左半部分所指元素 >= 右半部分所指元素
arr[k] = aux[j-l]; j ++;
}
}
}
public static void sort(Comparable[] arr){
int n = arr.length;
// Merge Sort Bottom Up 无优化版本
// for (int sz = 1; sz < n; sz *= 2)
// for (int i = 0; i < n - sz; i += sz+sz)
// // 对 arr[i...i+sz-1] 和 arr[i+sz...i+2*sz-1] 进行归并
// merge(arr, i, i+sz-1, Math.min(i+sz+sz-1,n-1));
// Merge Sort Bottom Up 优化
// 对于小数组, 使用插入排序优化
for( int i = 0 ; i < n ; i += 16 )
InsertionSort.sort(arr, i, Math.min(i+15, n-1) );
for( int sz = 16; sz < n ; sz += sz )
for( int i = 0 ; i < n - sz ; i += sz+sz )
// 对于arr[mid] <= arr[mid+1]的情况,不进行merge
if( arr[i+sz-1].compareTo(arr[i+sz]) > 0 )
merge(arr, i, i+sz-1, Math.min(i+sz+sz-1,n-1) );
}
// 测试 MergeSort BU
public static void main(String[] args) {
int N = 1000000;
Integer[] arr = SortTestHelper.generateRandomArray(N, 0, 100000);
SortTestHelper.testSort("bobo.algo.MergeSortBU", arr);
return;
}
}
自底向上的归并排序方法没有用到数组的索引,所以可以很好的对链表结构进行排序
Merge Sort BU 也是一个O(nlogn)复杂度的算法,虽然只使用两重for循环,所以,Merge Sort BU也可以在1秒之内轻松处理100万数量级的数据 注意:不要轻易根据循环层数来判断算法的复杂度,Merge Sort BU就是一个反例
快速排序 - QuickSort
基本思路: 以下图的数组为例,首先选定一个元素4,把它挪到当它在排好序的时候,应该处的位置,当它处在这个位置之后,使得这个数组有了一个性质:在4之前的数都小于4,在4之后的数都大于4。接下来,对小于4的子数组和大于4的子数组分别继续进行快速排序。这样逐渐递归,完成整个排序过程。
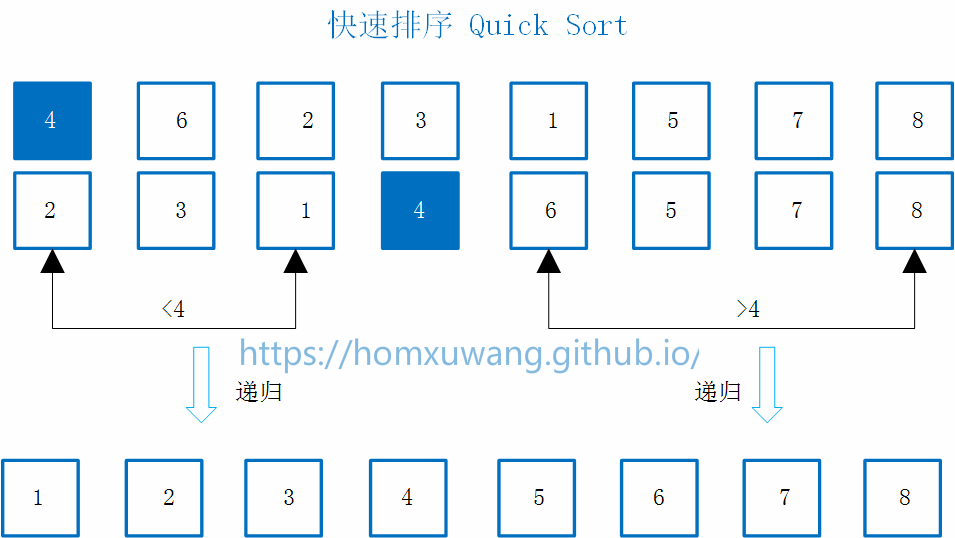
那么关键问题是怎么把4这个元素放在正确的改放的位置,这个过程称为Partition。 通常使用数组的第一个元素作为分界的标志点,第一个位置记作l,然后逐渐遍历右边没有被访问的元素,在遍历的过程中,逐步整理让元素一部分是>v一部分是<v的,将大于v和小于v的分界点的索引记为j,当前访问的元素e的索引记作i。 下面讨论i位置的e该如何处理,如图。如果e>v则将它放在这个位置不变,i++继续讨论下一个元素。否则如果e<v则将i位置的e与j+1位置的元素交换,j++,i++,继续考察下一个元素。 依次继续进行操作,直至遍历完数组的所有元素。 这时候要将v放在数组中合适的位置,即将索引l位置的v与索引j位置的元素进行交换。 最终完成此次操作。
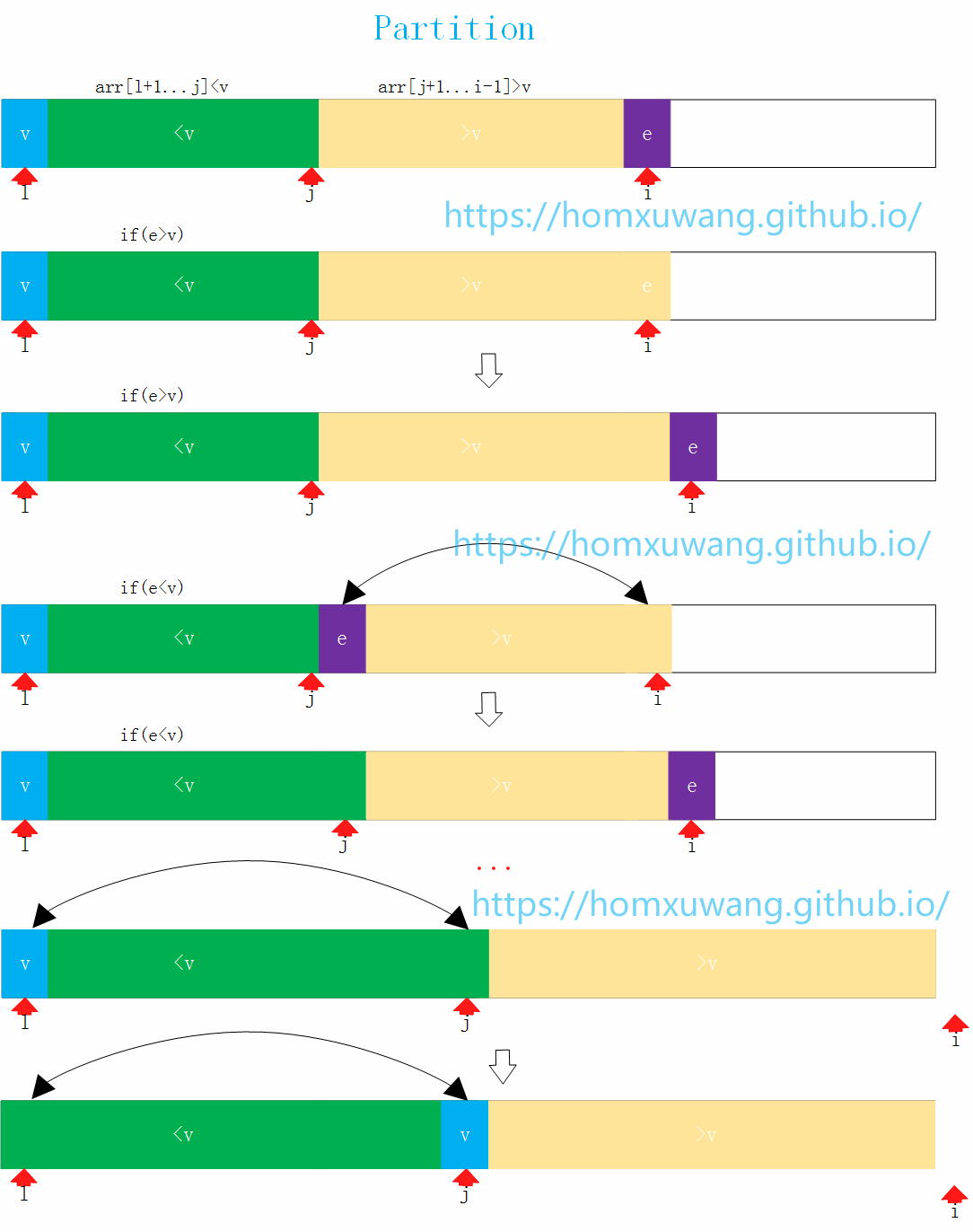 代码实现:
代码实现:
import java.util.*;
public class QuickSort {
// 我们的算法类不允许产生任何实例
private QuickSort(){}
// 对arr[l...r]部分进行partition操作
// 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p]
private static int partition(Comparable[] arr, int l, int r){
Comparable v = arr[l];
int j = l; // arr[l+1...j] < v ; arr[j+1...i) > v
for( int i = l + 1 ; i <= r ; i ++ )
if( arr[i].compareTo(v) < 0 ){
j ++;
swap(arr, j, i);
}
swap(arr, l, j);
return j;
}
// 递归使用快速排序,对arr[l...r]的范围进行排序
private static void sort(Comparable[] arr, int l, int r){
if( l >= r )
return;
int p = partition(arr, l, r);
sort(arr, l, p-1 );
sort(arr, p+1, r);
}
public static void sort(Comparable[] arr){
int n = arr.length;
sort(arr, 0, n-1);
}
private static void swap(Object[] arr, int i, int j) {
Object t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
}
Quick Sort也是一个O(nlogn)复杂度的算法 可以在1秒之内轻松处理100万数量级的数据
堆排序
排序算法总结
| 平均时间复杂度 | 原地排序 | 额外空间 | 稳定排序 | |
|---|---|---|---|---|
| 选择排序 Selection Sort | O(n^2) | √ | O(1) | × |
| 插入排序 Insertion Sort | O(n^2) | √ | O(1) | √ |
| 归并排序 Merge Sort | O(nlogn) | × | O(n) | √ |
| 快速排序 Quick Sort | O(nlogn) | √ | O(logn) | × |
| 堆排序 Heap Sort | O(nlogn) | √ | O(1) | × |
排序算法的稳定性:稳定排序是指对于相等的元素,在排序后,原来靠前的元素依然靠前。相等元素的相对位置没有发生改变。