最短路径问题
最短路径问题(Shortest Path)
本文的最短路径问题对于有向图也无线图都是成立的。常见应用:路径规划、工作任务规划。
在图的遍历-广度优先遍历中介绍的广度优先遍历的结果就是求出了一个最短路径。这种方法求的是从一个节点开始,到其他所有节点的最短路径,这样形成的是一个节点连接其他节点的树,即最短路径树(Shortest Path Tree).这棵树也是这个图的生成树,但是不是最小生成树,最小生成树是所有的边权值总和是最小的,而最短路径树是所有的节点距离起始节点的权值是最小的,这个求得最短路径树的过程,称为单源最短路径问题(Single Source Shortest Path).单源即是一个起始点的意思。这里是求出了从一个点到其他所有可以抵达的点的最短路径,不是两点间的最短路径。
下图中从0->2->1的操作称为松弛操作,即想计算到一个点的最短路径,尝试通过其他点”绕一下”,然后比较是否比直接到达要短。松弛操作是最短路径求解的核心。 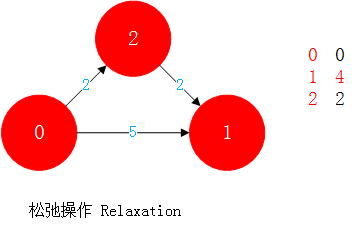
Dijkstra 单源最短路径算法
Dijkstra算法的前提:
- 图中不能有值为负的权重边
其时间复杂度为O(E log(V))
以下面的有向加权图为例,介绍Dijkstra单源最短路径算法.
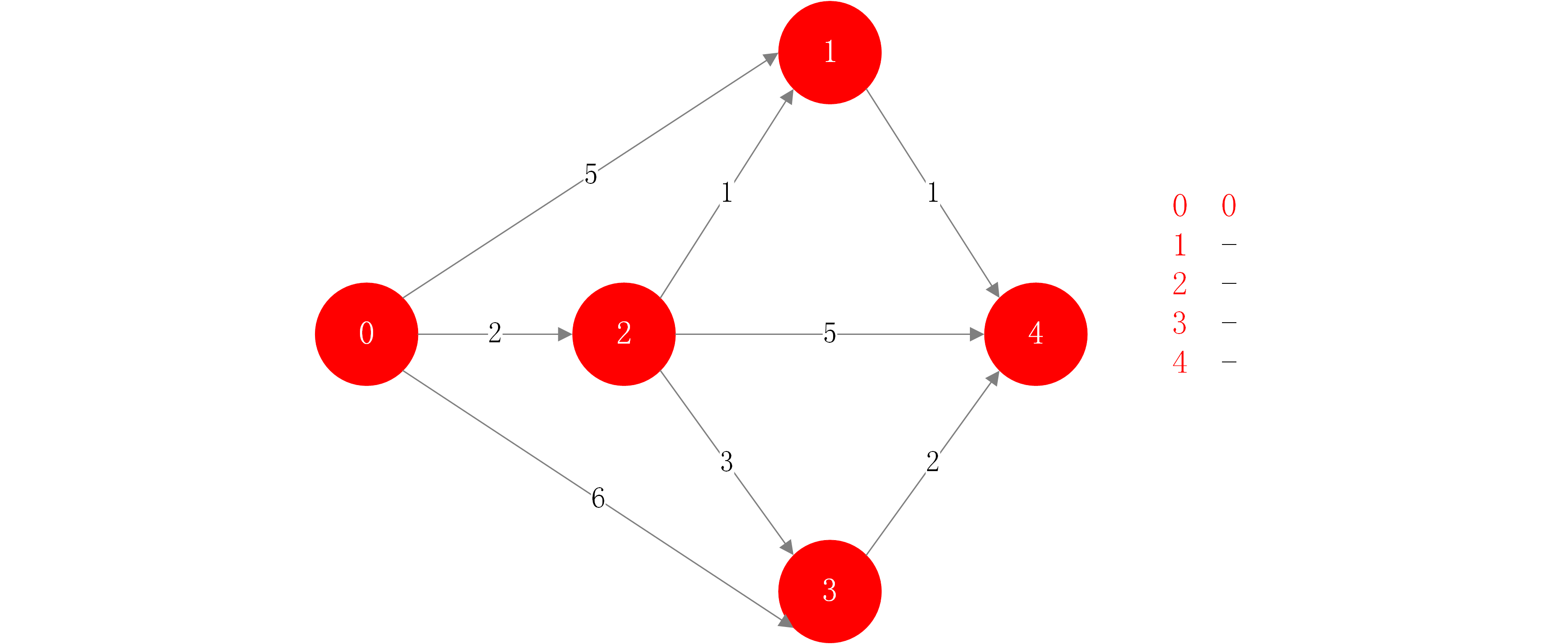
假设从点0开始,寻求0到其他所有点的最短路径。因为起点是0,所以0到0的最短路径是0. step1:首先对起点进行标识,然后对它所有的临边进行访问,同时更新数组.此时找到没有访问的节点中,能够以最短的方式抵达的节点(此时为节点2,它只需用权值为2的费用就可以抵达),则可以说,从源点到节点2的最短路径就是权值2.(因为2已经是所有能抵达的相邻的节点中最小的权值了)。
图中不能有负权边保证了这一前提的成立,因为没有负权边,所以即使通过别的边进行松弛操作,那么它们的权重之和也肯定也会大于该边
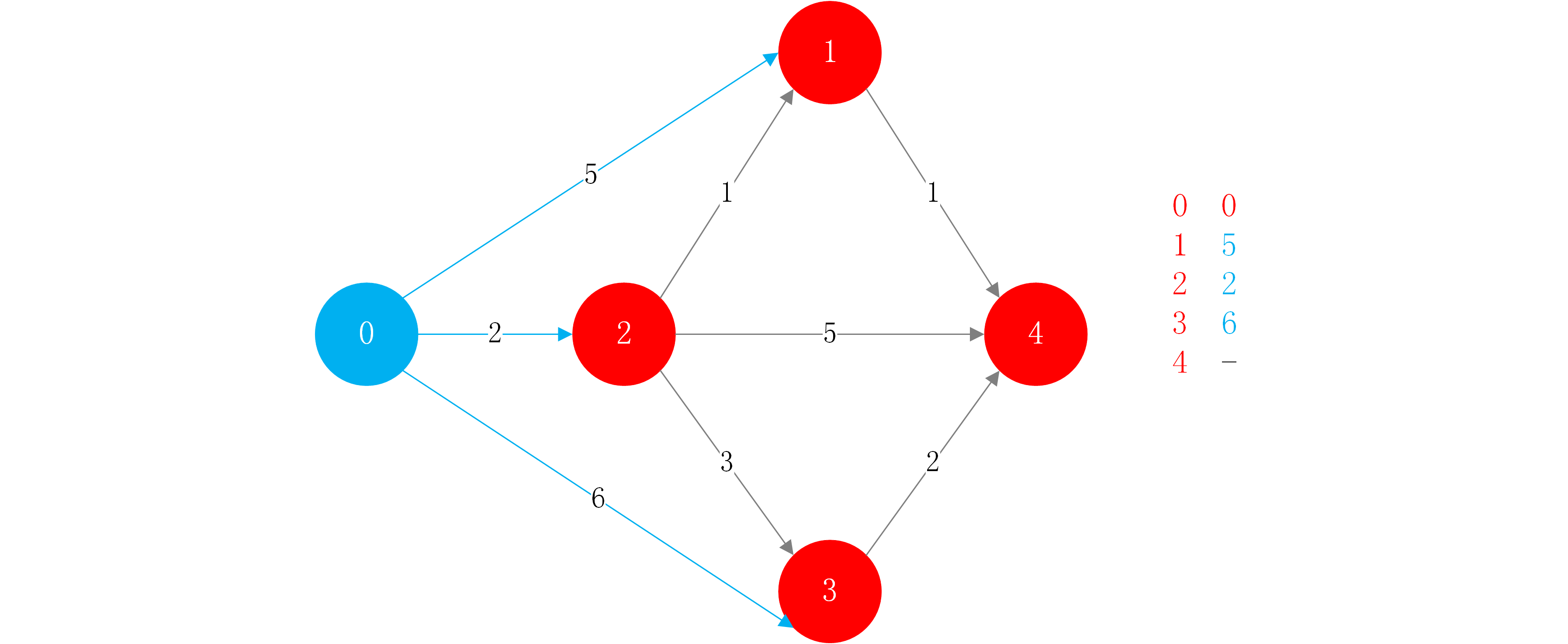
step2:找到了从源点到节点2的最短路径以后,下面就要进行松弛操作.即验证从源点通过节点2到其他节点的路径是否比源点直接到达其他节点的路径要短。
开始看节点2的所有临边。
第一条临边为2->1的边,从源点到节点2权值为2,从节点2到节点1权值为1,总权重为3<5.所以0->1的最短路径为0->2->1 = 3.所以可以在数组中更新对应的最短路径。
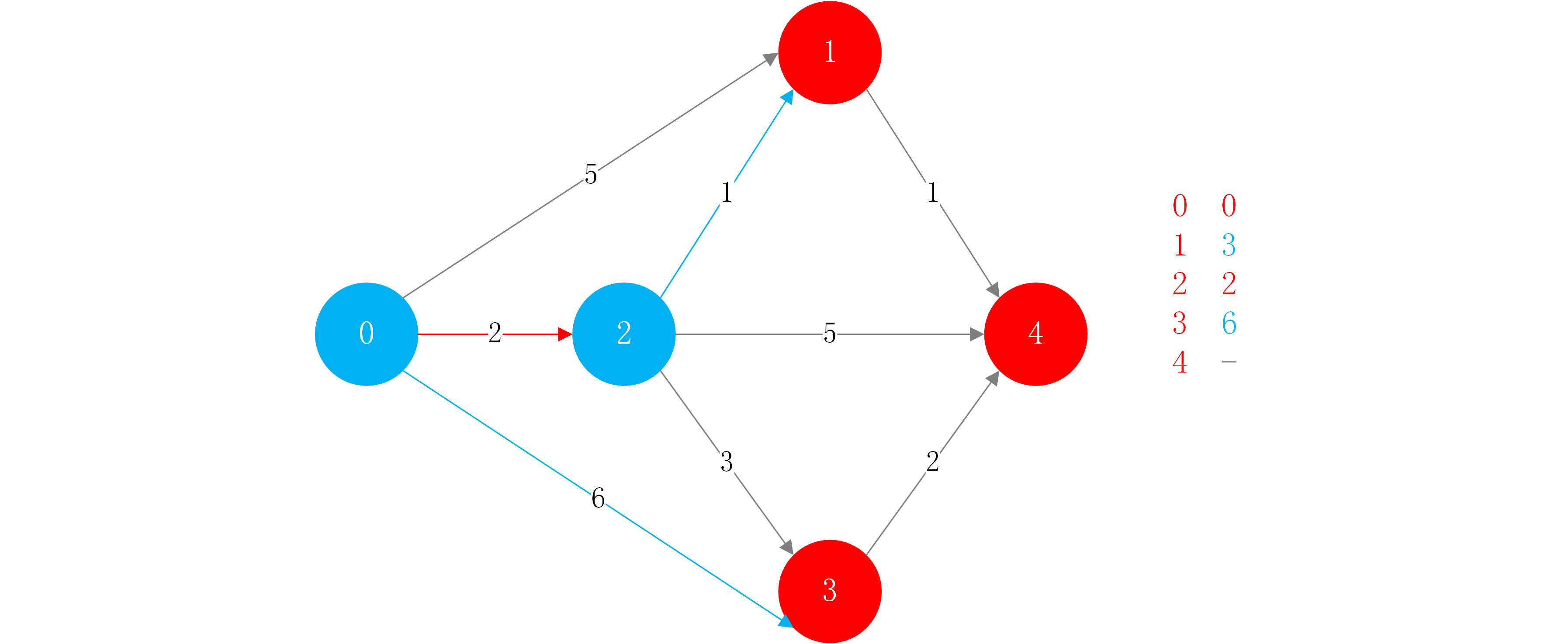
接下来看节点2的下一个相邻节点节点4.因为节点4还没被访问过,所以从源点到节点4找到了一条权重为7的路径,在数组中进行记录。
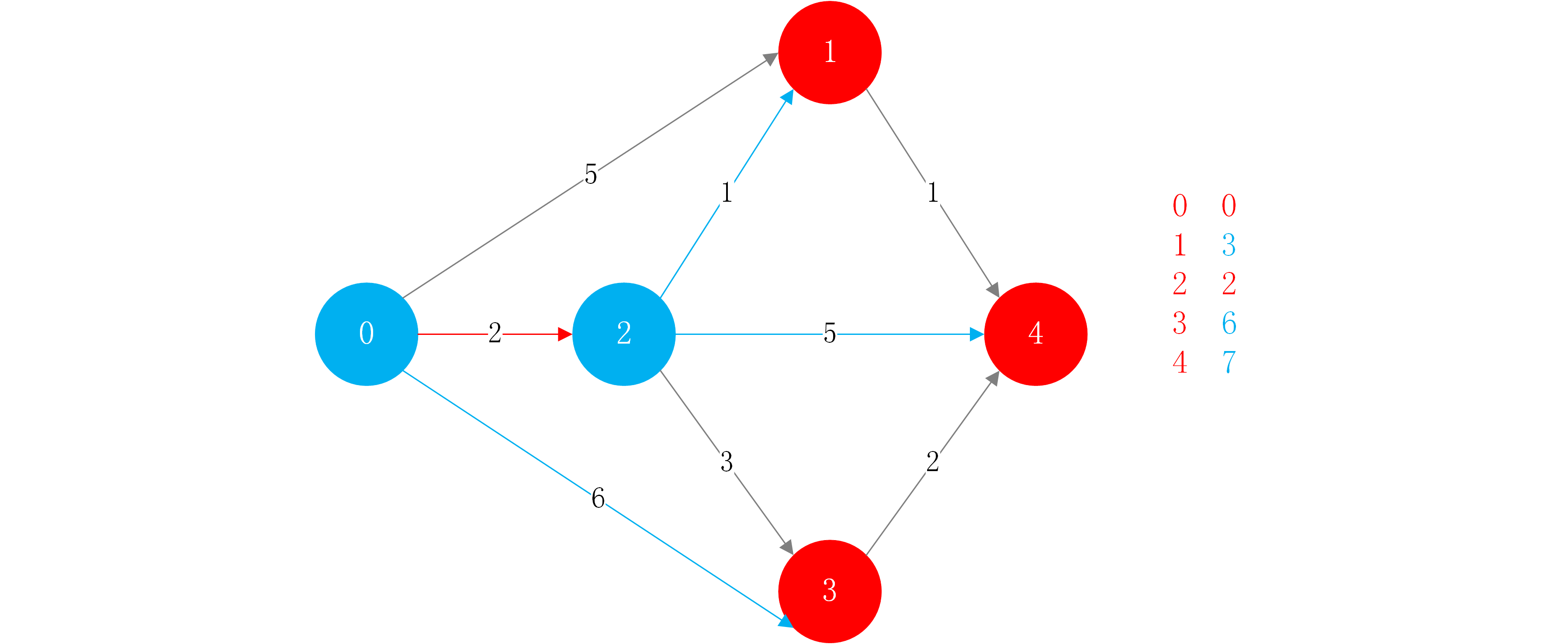
然后接着看2->3.从2->3的权值为3,从0->2->3的权重为5.小于从0->3的权重6.这时候完成了Dijkstra算法的一轮循环.
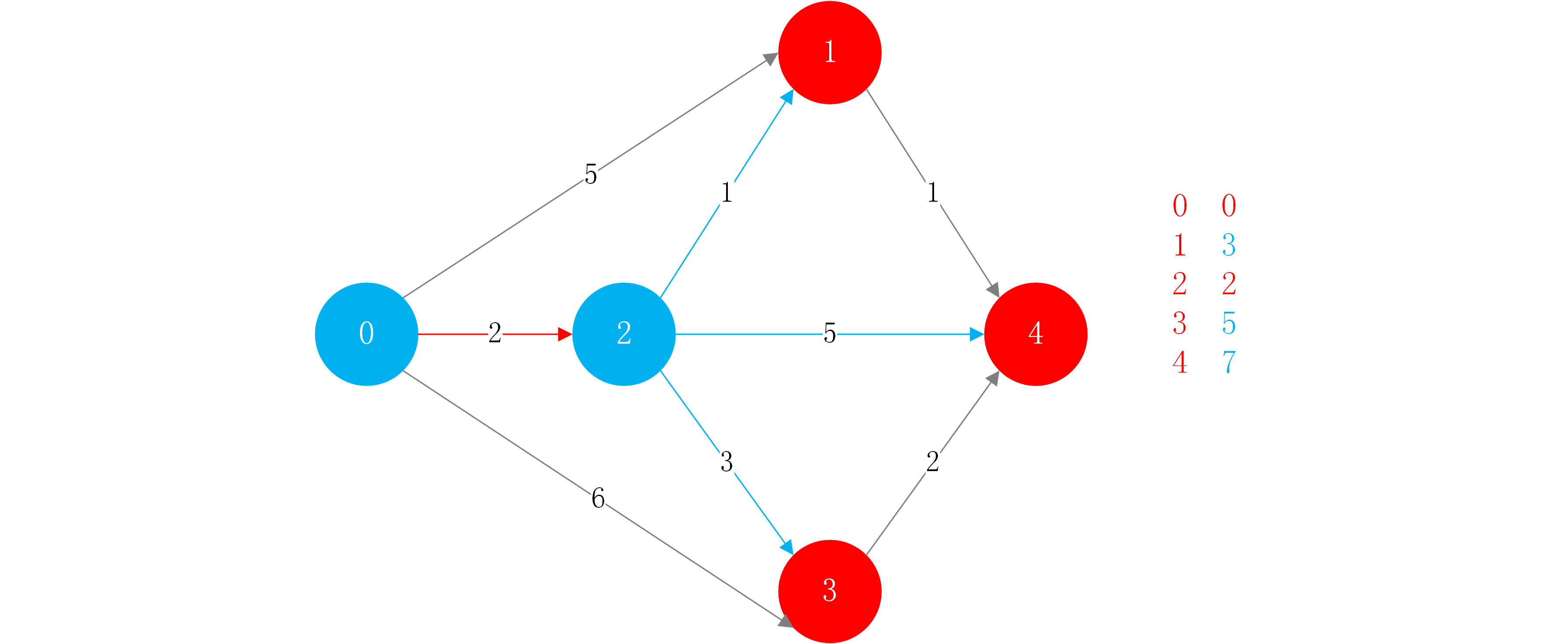
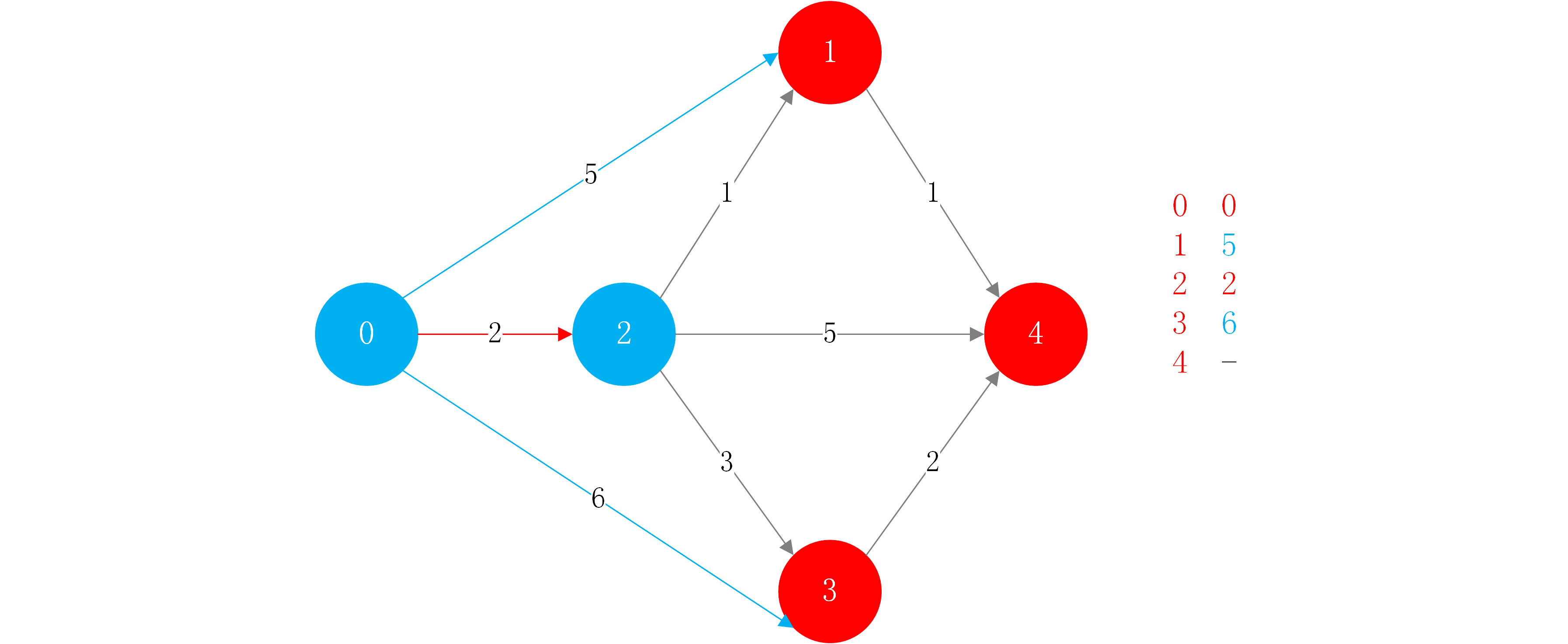
step3:接着找到此时还没有找到最短路径的节点中,现在存的最短的路径能抵达的节点是谁,此时为节点1(权值为3).则可以说0->2->1就是从0到1的最短路径.
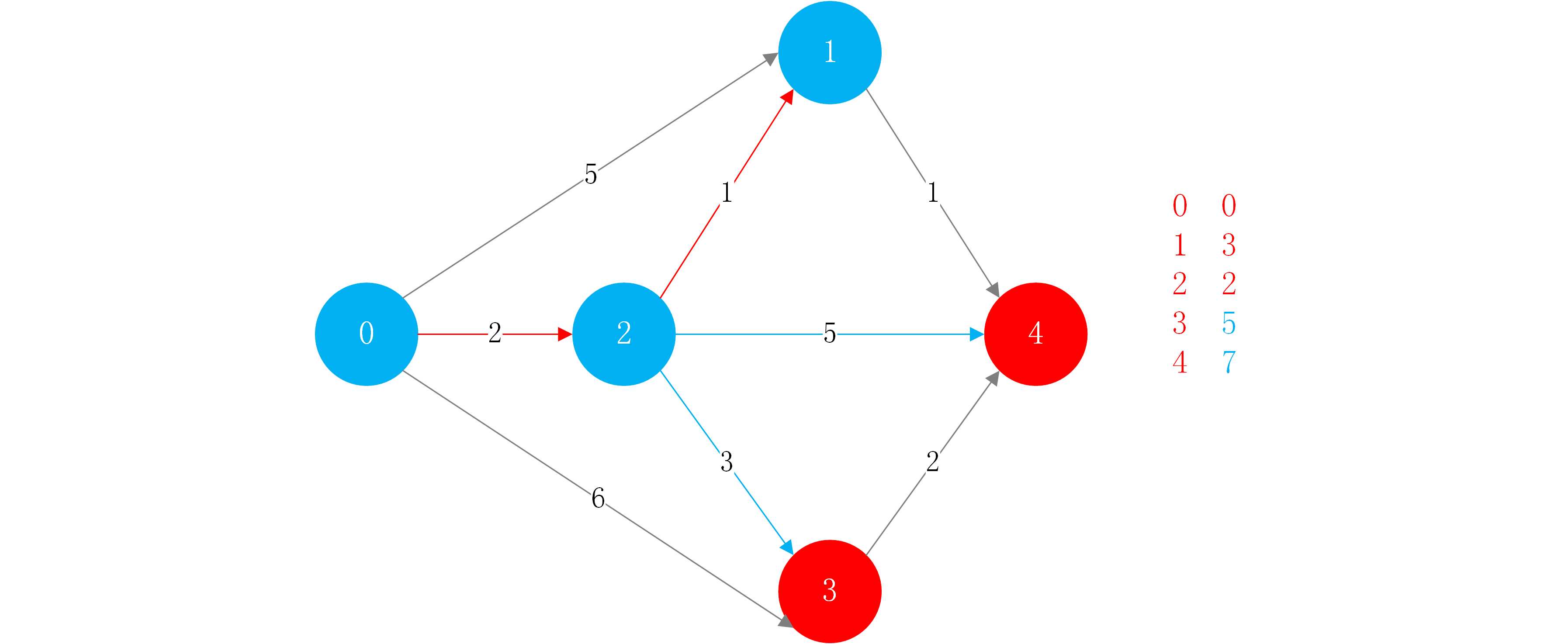
然后根据节点1的临边,进行松弛操作。此时为1->4的临边,其权值为1.由于0->1的最短路径为3,1->4的路径为1,此时经过1到达4的路径总长度为4.小于7.所以可以将从源点到节点4的路径长度更新为4.之前指向4的边就可以废弃不用了,它一定不是一条最短路径。此时和1相邻的边的松弛操作就做完了。
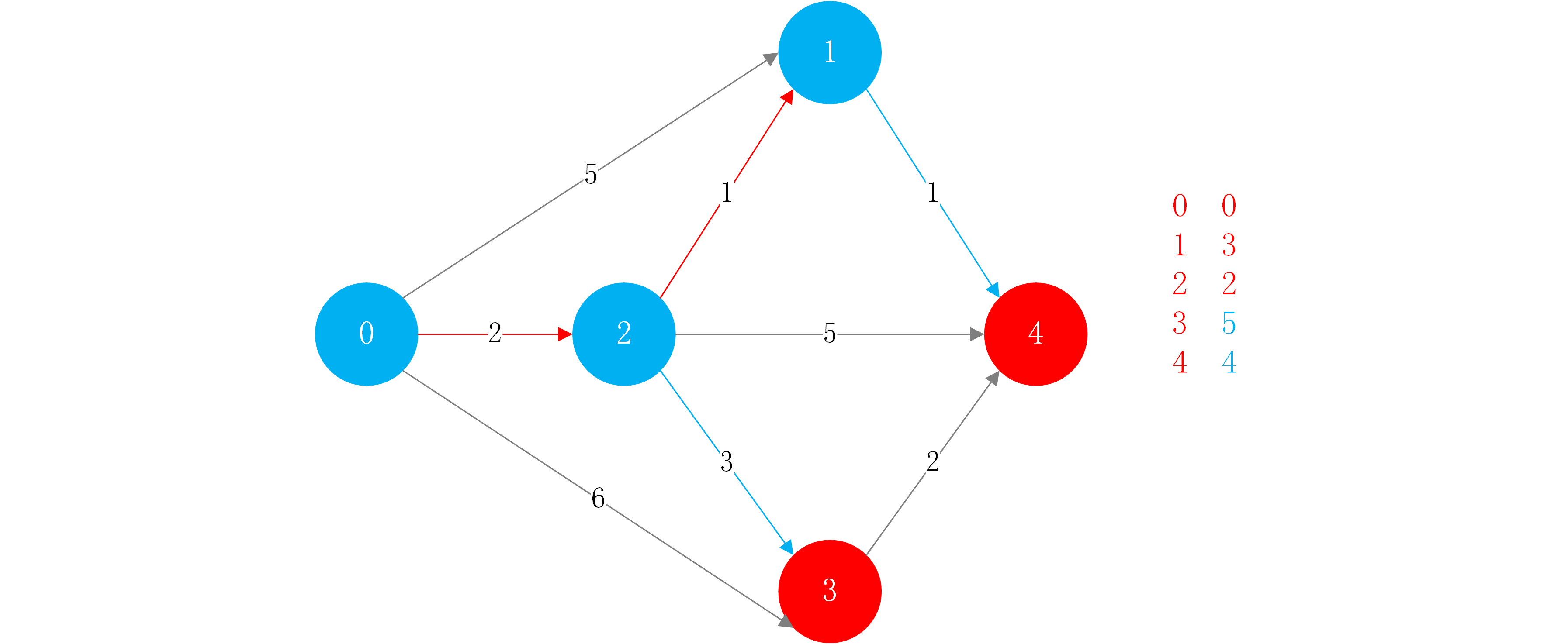
下面只有节点3和节点4没有访问到,此时最短的路径是到4,它的权值是4,从1->4的最短路径就是4.
然后对针对节点4,对节点4的所有邻边进行松弛操作.但是4无法到其他任何节点,所以此时不需要进行操作.
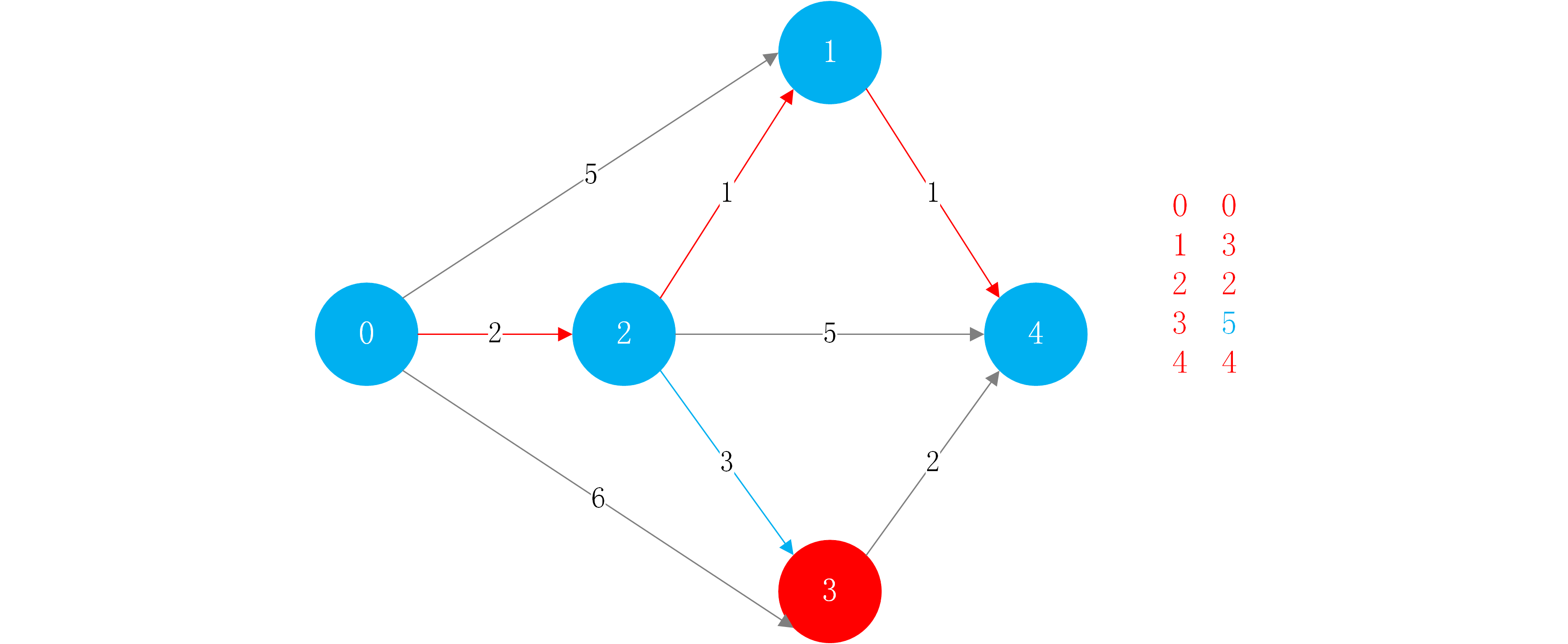
step4:最后只剩下节点3没有访问过,此时没有其他选择,即现在的0->2->3即为0->3的最短路径.
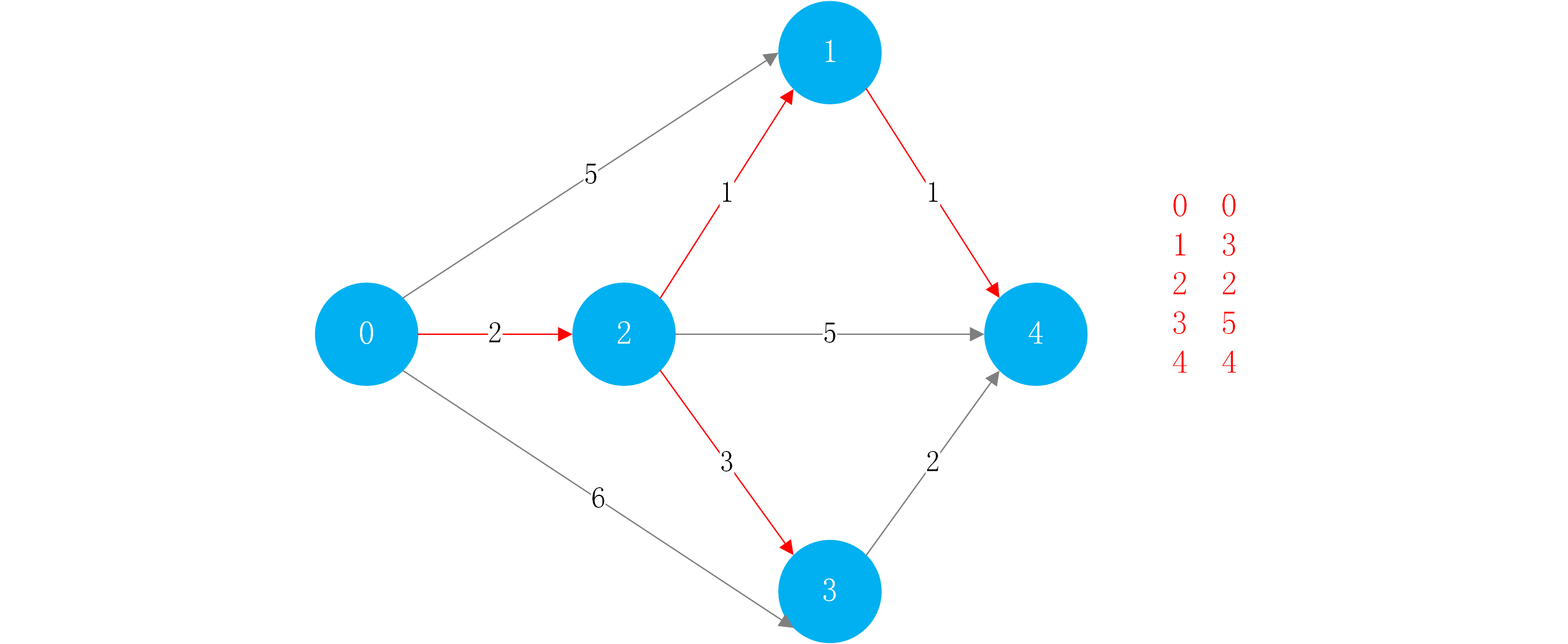
此时就完成了Dijkstra算法.找到了一个以节点0为根的最短路径树.
算法总结和实现细节:
- 对路径的记录都是在右侧的列表操作.第一个操作是找到没有访问过的节点中的最短的路径相应的节点.第二个操作是更新列表.可以借用IndexMinHeap实现该操作.开辟节点个数的空间.每次的插入和更新操作都是O(logV)的时间复杂度.Dijkstra的整个操作对所有的边进行遍历,最终的时间复杂度为O(ElogV).
Dijkstra算法实现
程序的目录结构 
相关参考代码: 堆和堆排序 图的表达 最小索引堆 ReadWeightedGraph.java有实现代码
Dijkstra算法的具体实现代码见附录1
处理负权边
如图所示,如果引入了负权边,那么在没有负权边的情况下进行松弛操作之前就能确定一个最短边,现在则是有可能“绕路”的情况要比直接到达的情况效率更高。可以看出,它计算0->1->2的操作仍然依赖了松弛操作。
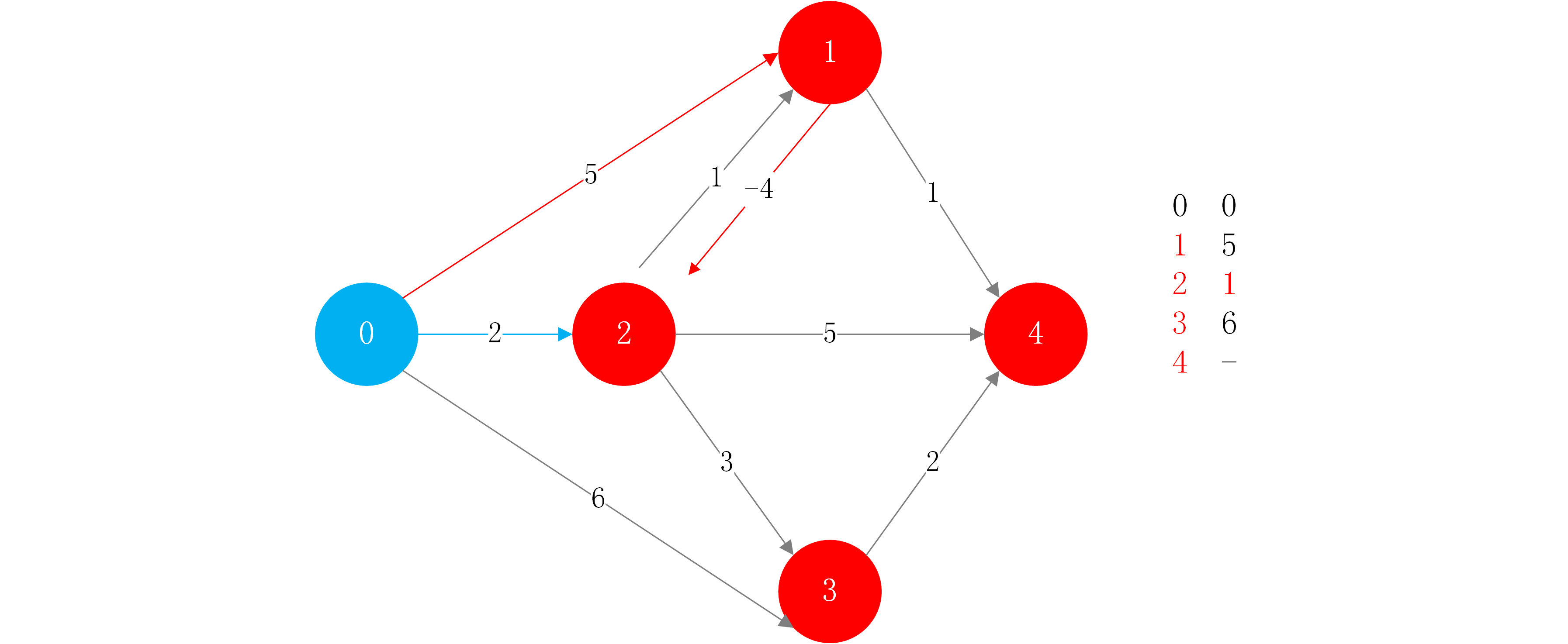
当然,负权边会产生一个问题,如图。下图多了一条从2->0的负权边,这样就形成了一个负权环.如果一个图中出现了负权环,那么寻找一点到另一点的最短路径,只要经过了负权环,那么它就会在环中不断“循环”,因为在环中每转一次,那么最短路径都会减少.所以这样就无法计算出最短路径了(或最短路径为负无穷).
那么可以得出一个结论:拥有负权环的图没有最短路径.
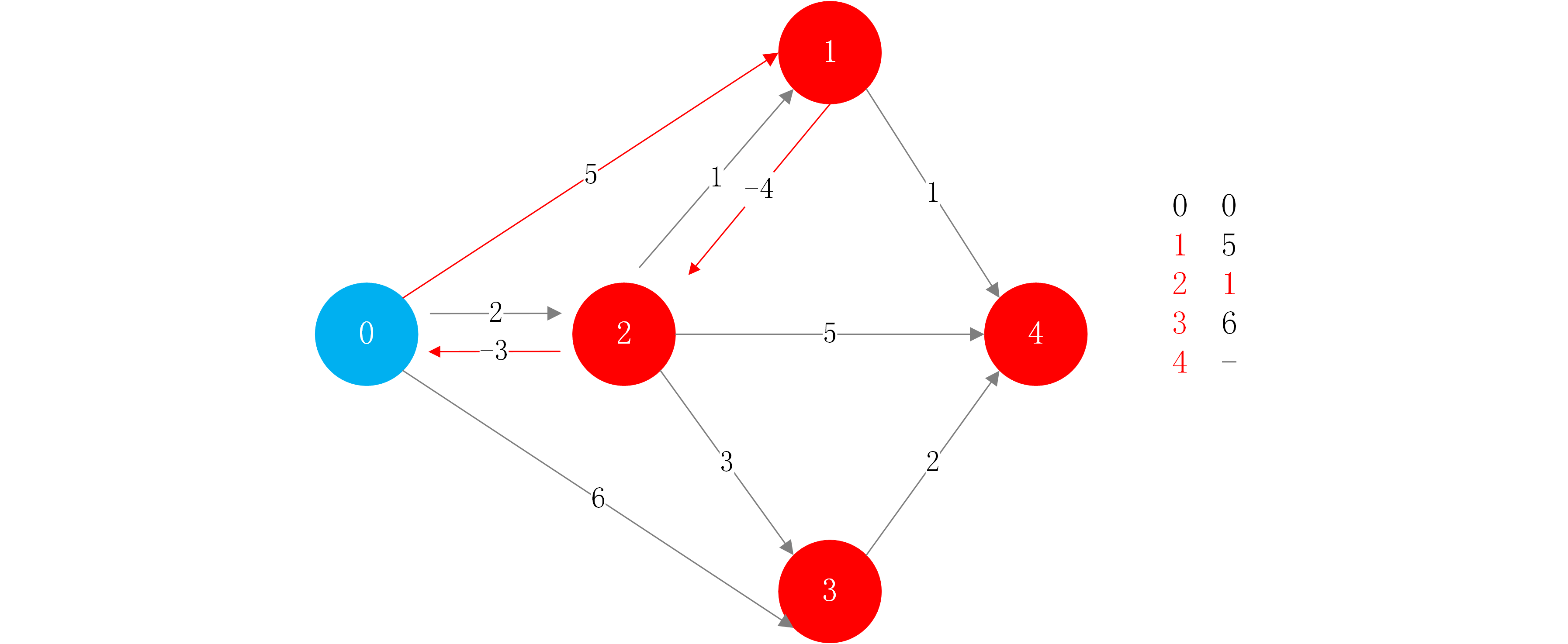
两个结点也可以构成负权环,如下图的节点1和2:
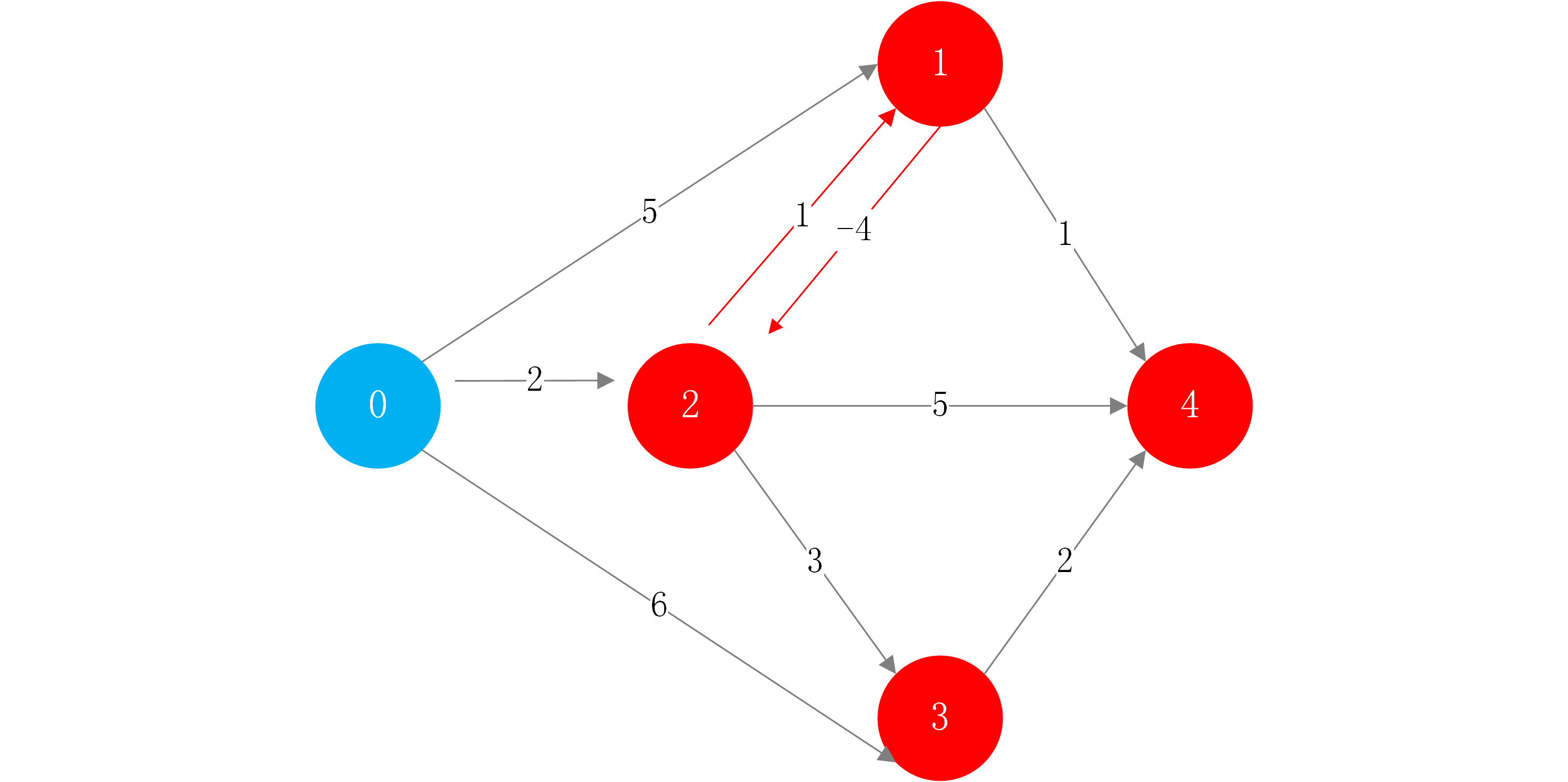
Bellman-Ford 单源最短路径算法
该算法的前提是,图中可以有负权边,但是不能有负权环
Bellman-Ford可以判断图中是否有负权环,不过因此它的时间复杂度为O(EV).
Bellman-Ford的算法思想,如果一个图没有负权环,那么从一个点(起始点)到另一个点的最短路径,最多经过所有的顶点,有V-1条边.否则,则存在一个顶点经过了两次,说明存在负权环.
如下图,存在两个负权边.
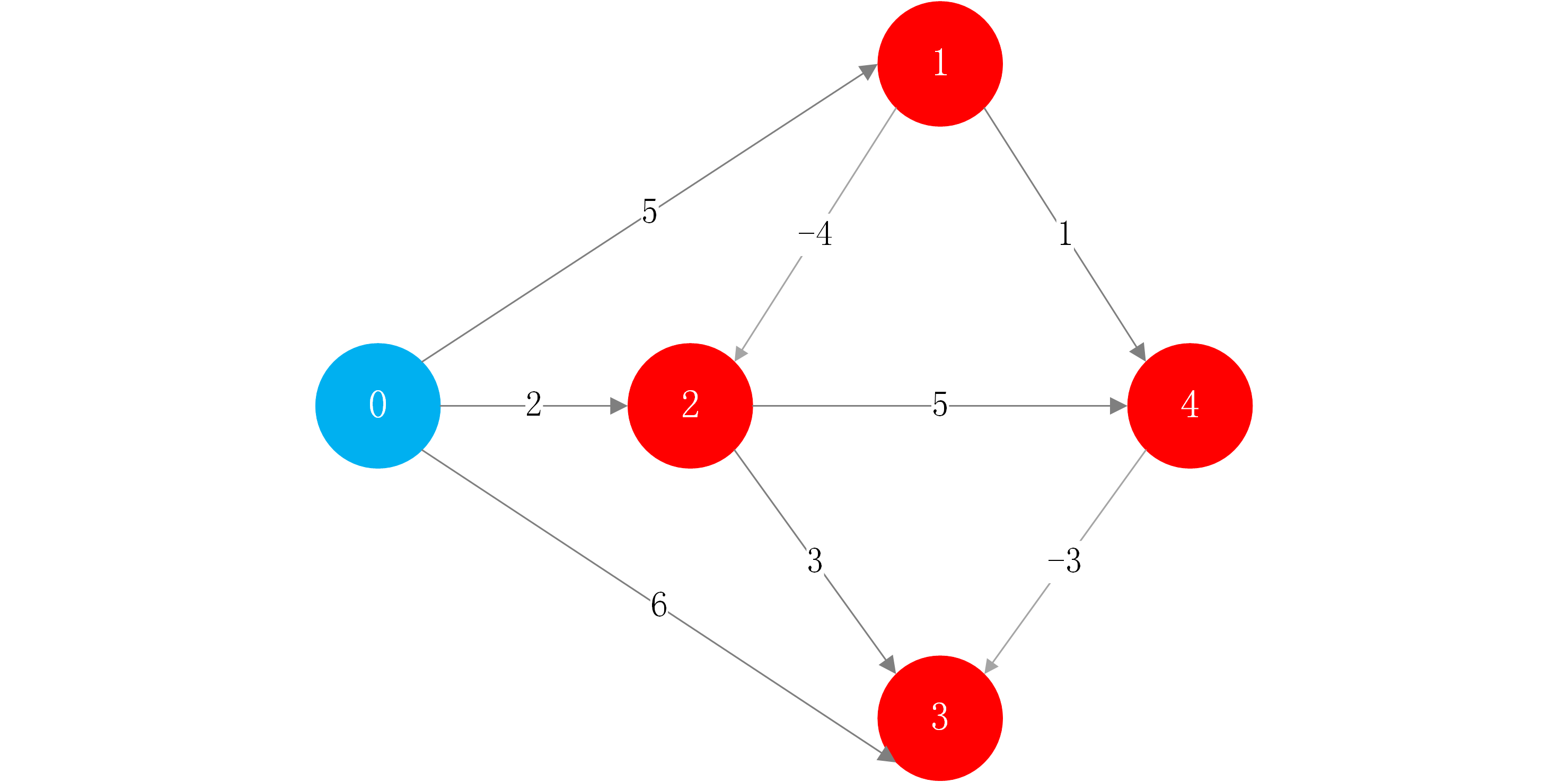
step1:找到所有节点0的临边,那么暂时找到了从0到其相邻顶点的最短路径.从另一个角度来看待节点0的所有临边,相当于对0的相应的所有的节点进行了一次松弛操作,这次操作的结果得到了从原点开始,经过1条边到达其他节点的最短路径.
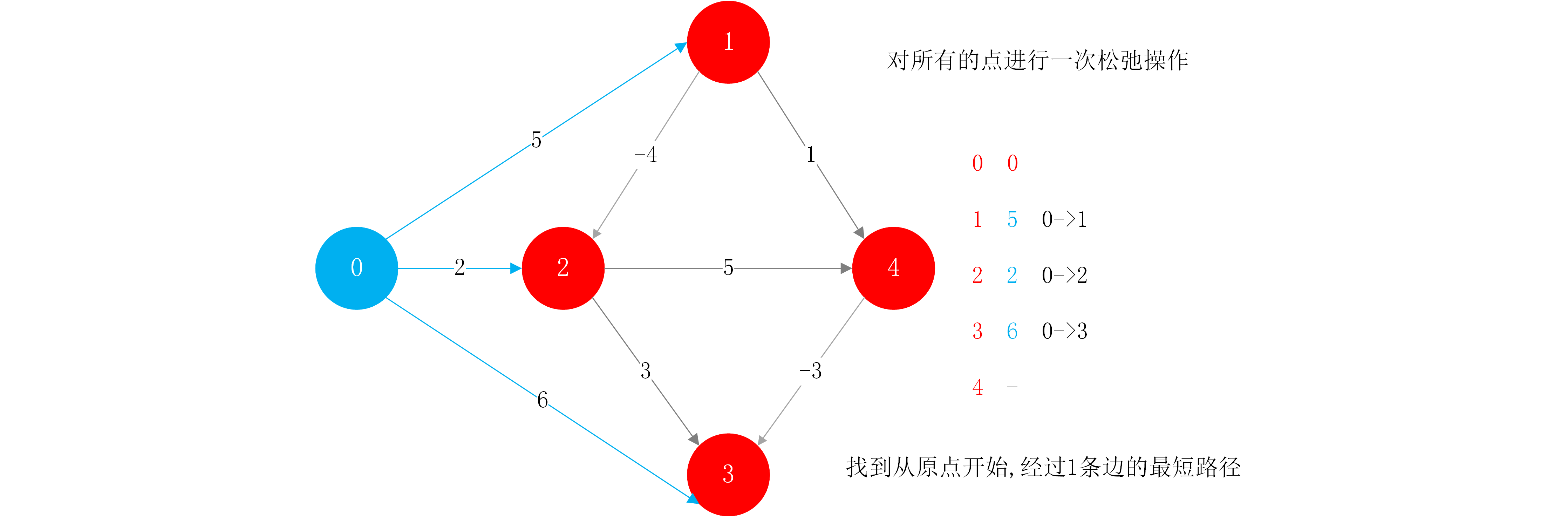
step2:对所有的点进行第2次松弛操作(这里记住松弛操作的核心思想就是尝试从一个点出发中间经过一个点到达目的点的路径是否会更短.即找一个两条边的路径,看其权值是否会比只有一条边的路径权值更小)。结合本例,第二次松弛操作就找到了从节点0到节点2更短的路径.
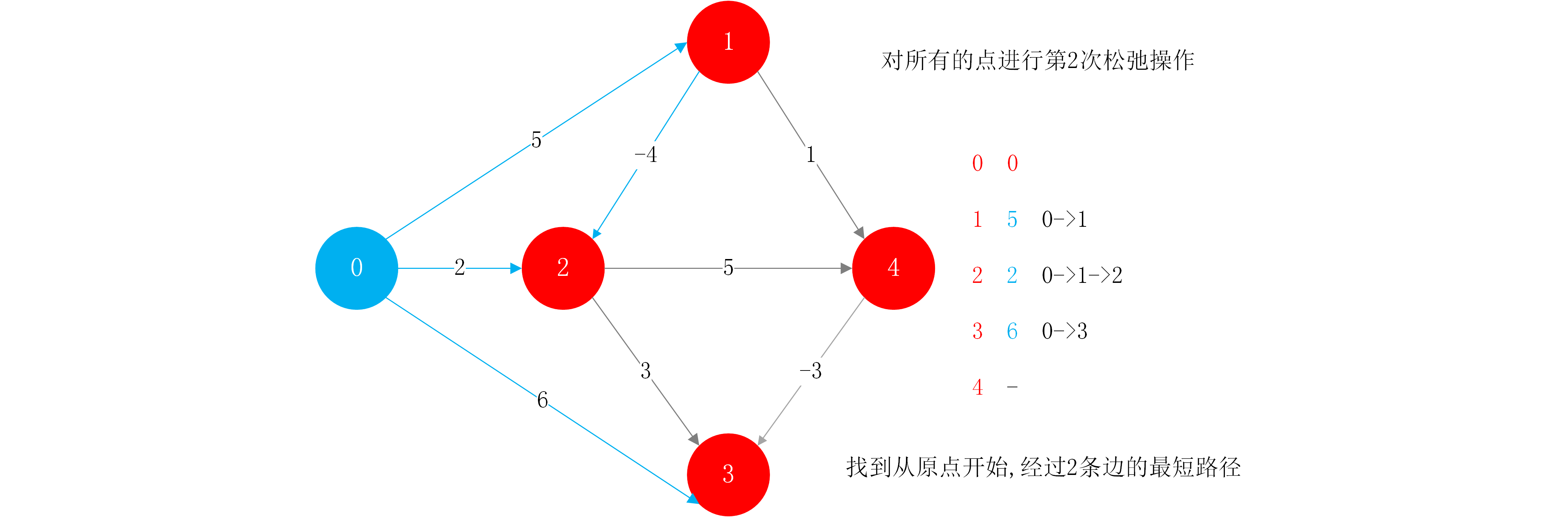
对一个点的一次松弛操作,就是找到经过这个点的另外一条路径,多一条边,权值会更小.
前面提到过,如果一个图没有负权环,那么从一个点(起始点)到另一个点的最短路径,最多经过所有的顶点,有V-1条边.否则,则存在一个顶点经过了两次,说明存在负权环.
如果对所有的点都进行V-1次松弛操作,理论上就找到了从源点到其他所有点的最短路径.也即Bellman-Ford的主体思想就是对所有的点进行V-1次松弛操作.
如果还可以进行松弛操作(也就是进行第V轮松弛操作),那么说明原图中有负权环.
对所有点进行松弛操作,每个边都要遍历一遍,时间复杂度为O(E).这样的操作要进行V轮,所以其时间复杂度为O(EV).
Bellman-Ford 代码实现
BellmanFord的实现代码和两个图的表达见附录2
Bellman-Ford代码的优化和其他算法
可以使用队列进行相应优化,比如queue-based bellman-ford算法.
| 算法 | 要求 | 要求 | 复杂度 |
|---|---|---|---|
| dijkstra | 无负权边 | 有向无向图均可 | O(ElogV) |
| Bellman-Ford | 无负权环 | 有向图 | O(VE) |
| 利用拓扑排序 | 有向无环图 DAG | 有向图 | O(V+E) |
所有对最短路径算法,可以回答任何一个点到其他任何点的最短路径.可以用Floyed算法实现,处理无负权环的图O(V^3)
对于最长路径问题,最长路径问题不能有正权环。无权图的最长路径问题是指数级难度的。对于有权图,不能使用Dijkstra求最长路径问题,但是可以使用Bellman-Ford算法.
附录1-Dijkstra算法实现
Dijkstra算法实现代码
import java.util.Vector;
import java.util.Stack;
// Dijkstra算法求最短路径
public class Dijkstra<Weight extends Number & Comparable> {
private WeightedGraph G; // 图的引用
private int s; // 起始点
private Number[] distTo; // distTo[i]存储从起始点s到i的最短路径长度
private boolean[] marked; // 标记数组,在算法运行过程中标记节点i是否被访问
private Edge<Weight>[] from; // from[i]记录最短路径中,到达i节点的边是哪一条,可以用来恢复整个最短路径
//构造函数,使用Dijkstra算法求最短路径
public Dijkstra(WeightedGraph graph, int s){
//算法初始化
G = graph;
if(s < 0 || s > G.V()){
throw new IllegalArgumentException("s is out of bounds!");
}
this.s = s;
distTo = new Number[G.V()];
marked = new boolean[G.V()];
from = new Edge[G.V()];
for (int i = 0 ; i < G.V() ; i ++) {
distTo[i] = 0.0;
marked[i] = false;
from[i] = null;
}
// 使用索引堆记录当前找到的到达每个顶点的最短距离
IndexMinHeap<Weight> ipq = new IndexMinHeap<Weight>(G.V());
//对于起始点s进行初始化
distTo[s] = 0.0;
from[s] = new Edge<Weight>(s, s, (Weight)(Number)0.0);
ipq.insert(s,(Weight)distTo[s]);
marked[s] = true;
while (!ipq.isEmpty()){
int v = ipq.extractMinIndex();
// distTo[v]就是s到v的距离
marked[v] = true;
// 对v的所有相邻节点进行更新,即松弛操作
for( Object item : G.adj(v) ){
Edge<Weight> e = (Edge<Weight>) item;
int w = e.other(v);
//如果从s点到w点的最短路径还没有找到
if( !marked[w] ){
//如果w点以前没有访问过
//或者访问过,但是通过当前的v点到w点距离更短,则进行更新
if( from[w] == null || distTo[v].doubleValue() + e.wt().doubleValue() < distTo[w].doubleValue() ){
//长度更新为较小的值
distTo[w] = distTo[v].doubleValue() + e.wt().doubleValue();
//对from进行更新
from[w] = e;
//对最小索引堆进行判断
if( ipq.contain(w) ){
ipq.change(w,(Weight)distTo[w]);
}
else{
ipq.insert(w,(Weight)distTo[w]);
}
}
}
}
}
}
// 返回从s点到w点的最短路径长度
Number shortestPathTo( int w ){
if(w < 0 || w >= G.V() ){
throw new IllegalArgumentException("w is out of bounds!");
}
if(!hasPathTo(w)){
throw new IllegalArgumentException("these two have no path!");
}
return distTo[w];
}
//判断从s点到w点是否联通
boolean hasPathTo( int w ){
if(w < 0 || w >= G.V() ){
throw new IllegalArgumentException("w is out of bounds!");
}
return marked[w];
}
//寻找从s到w的最短路径,将整个路径经过的边存放在vec中
Vector<Edge<Weight>> shortestPath( int w ){
if(w < 0 || w >= G.V() ){
throw new IllegalArgumentException("w is out of bounds!");
}
if(!hasPathTo(w)){
throw new IllegalArgumentException("these two have no path!");
}
//通过from数组逆向查找到从s到w的路径,存放到栈中
Stack<Edge<Weight>> s = new Stack<>();
Edge<Weight> e = from[w];
while( e.v() != this.s ){
s.push(e);
e = from[e.v()];
}
s.push(e);
//从栈中依次取出元素,获得顺序的从s到w的路径
Vector<Edge<Weight>> res = new Vector<>();
while (!s.empty()){
e = s.pop();
res.add(e);
}
return res;
}
//打印出从s点到w点的路径
void showPath(int w){
if(w < 0 || w >= G.V() ){
throw new IllegalArgumentException("w is out of bounds!");
}
if(!hasPathTo(w)){
throw new IllegalArgumentException("these two have no path!");
}
Vector<Edge<Weight>> path = shortestPath(w);
for (int i = 0 ; i < path.size(); i ++){
System.out.print(path.elementAt(i).v() + "->");
if( i == path.size() - 1)
System.out.println(path.elementAt(i).w());
}
}
}
测试用的图文件testG1.txt
5 8
0 1 5
0 2 2
0 3 6
1 4 1
2 1 1
2 4 5
2 3 3
3 4 2
Main函数中测试:
public class Main {
// 测试Dijkstra最短路径算法
public static void main(String[] args) {
String filename = "testG1.txt";
int V = 5;
SparseWeightedGraph<Integer> g = new SparseWeightedGraph<Integer>(V, true);
// Dijkstra最短路径算法同样适用于有向图
//SparseGraph<int> g = SparseGraph<int>(V, false);
ReadWeightedGraph readGraph = new ReadWeightedGraph(g, filename);
System.out.println("Test Dijkstra:\n");
Dijkstra<Integer> dij = new Dijkstra<Integer>(g,0);
for( int i = 1 ; i < V ; i ++ ){
if(dij.hasPathTo(i)) {
System.out.println("Shortest Path to " + i + " : " + dij.shortestPathTo(i));
dij.showPath(i);
}
else
System.out.println("No Path to " + i );
System.out.println("----------");
}
}
}
测试结果
Test Dijkstra:
Shortest Path to 1 : 3.0
0->2->1
----------
Shortest Path to 2 : 2.0
0->2
----------
Shortest Path to 3 : 5.0
0->2->3
----------
Shortest Path to 4 : 4.0
0->2->1->4
----------
附录2-Bellman-Ford 代码实现
BellmanFord.java
import java.util.Vector;
import java.util.Stack;
// 使用BellmanFord算法求最短路径
public class BellmanFord<Weight extends Number & Comparable> {
private WeightedGraph G; //图的引用
private int s; //设置起始点
private Number[] distTo; //distT[i]存放从起始点s到i的最短路径长度
Edge<Weight>[] from; //from[i]记录最短路径中,到达i点的边是哪一条
//可以用来回复整个最短路径
boolean hasNegativeCycle; //标记图中是否有负权环
//构造函数,使用BellanFord算法求最短路径
public BellmanFord(WeightedGraph graph, int s){
G = graph;
this.s = s;
distTo = new Number[G.V()];
from = new Edge[G.V()];
//初始化所有的节点s都不可达,由from数组来表示
for(int i = 0 ; i < G.V() ; i ++){
from[i] = null;
}
//设置distTo[s]=0 ,并且让from[s]不为NULL,表示初始s节点可达且距离为0
distTo[s] = 0.0;
from[s] = new Edge<Weight>(s,s,(Weight)(Number)0.0);
//Bellman-Ford过程
//进行V-1次循环,每一次循环求出从起点到其余所有点,最多使用pass步可以到达的最短距离
for( int pass = 1 ; pass < G.V() ; pass ++){
//每次循环中对所有的边进行一遍松弛操作
//遍历所有边的方式是先遍历所有的顶点,然后遍历和所有顶点相邻的所有边
for( int i = 0 ; i < G.V() ; i ++){
//使用临边迭代器遍历和所有顶点相邻的所有边
for( Object item : G.adj(i) ){
Edge<Weight> e = (Edge<Weight>) item;
//对于每一个边首先判断e.v()可达
//之后看如果e.w()以前没有到达过,显然可以更新distTo[e.w()]
//或者e.w()以前虽然到达过,但是通过这个e可以获得一个更短的距离,即可以进行一次松弛操作,也可以更新distTo[e.w()]
if(from[e.v()] != null && (from[e.w()] == null || distTo[e.v()].doubleValue() + e.wt().doubleValue() < distTo[e.w()].doubleValue()) ){
distTo[e.w()] = distTo[e.v()].doubleValue() + e.wt().doubleValue();
from[e.w()] = e;
}
}
}
hasNegativeCycle = detectNegativeCycle();
}
}
//判断图中是否有负权环
boolean detectNegativeCycle() {
for(int i = 0 ; i < G.V() ; i ++){
for(Object item : G.adj(i) ){
Edge<Weight> e = (Edge<Weight>)item;
if( from[e.v()] != null && distTo[e.v()].doubleValue() + e.wt().doubleValue() < distTo[e.w()].doubleValue())
return true;
}
}
return false;
}
//返回图中是否有负权环
boolean negativeCycle() {
return hasNegativeCycle;
}
//返回从s点到w点的最短路径长度
Number shortestPathTo(int w){
if(w < 0 || w >= G.V()){
throw new IllegalArgumentException("w is out of bounds!");
}
if (hasNegativeCycle){
throw new IllegalArgumentException("this Graph hasNegativeCycle!");
}
if(!hasPathTo(w)){
throw new IllegalArgumentException(s + "to "+ w +"doesn't have path!");
}
return distTo[w];
}
//判断s点到w点是否联通
boolean hasPathTo(int w){
if(w < 0 || w >= G.V()){
throw new IllegalArgumentException("w is out of bounds!");
}
return from[w] != null;
}
//寻找s点到w点的最短路径,将整个路径经过的边存放在vec中
Vector<Edge<Weight>> shortestPath(int w){
if(w < 0 || w >= G.V()){
throw new IllegalArgumentException("w is out of bounds!");
}
if (hasNegativeCycle){
throw new IllegalArgumentException("this Graph hasNegativeCycle!");
}
if(!hasPathTo(w)){
throw new IllegalArgumentException(s + "to "+ w +"doesn't have path!");
}
//通过from数组逆向查找到从s到w的路径,存放到栈中
Stack<Edge<Weight>> s = new Stack<>();
Edge<Weight> e = from[w];
while (e.v() != this.s){
s.push(e);
e = from[e.v()];
}
s.push(e);
//从栈中依次取出元素,获得顺序的从s到w的路径
Vector<Edge<Weight>> res = new Vector<>();
while (!s.empty()){
e = s.pop();
res.add(e);
}
return res;
}
//打印出从s点到w点的路径
void showPath(int w) {
if(w < 0 || w >= G.V()){
throw new IllegalArgumentException("w is out of bounds!");
}
if (hasNegativeCycle){
throw new IllegalArgumentException("this Graph hasNegativeCycle!");
}
if(!hasPathTo(w)){
throw new IllegalArgumentException(s + "to "+ w +"doesn't have path!");
}
Vector<Edge<Weight>> res = shortestPath(w);
for(int i = 0 ; i < res.size() ; i ++){
System.out.print(res.elementAt(i).v() + " -> ");
if( i == res.size() - 1 ){
System.out.println(res.elementAt(i).w());
}
}
}
}
testG2.txt:
5 8
0 1 5
0 2 2
0 3 6
1 2 -4
1 4 2
2 4 5
2 3 3
4 3 -3
testG_negative_circle.txt
5 9
0 1 5
0 2 2
0 3 6
1 2 -4
2 1 1
1 4 2
2 4 5
2 3 3
4 3 -3
Main测试函数
public class Main {
// 测试我们的Bellman-Ford最短路径算法
public static void main(String[] args) {
String filename = "testG2.txt";
// String filename = "testG_negative_circle.txt";
int V = 5;
SparseWeightedGraph<Integer> g = new SparseWeightedGraph<Integer>(V, true);
ReadWeightedGraph readGraph = new ReadWeightedGraph(g, filename);
System.out.println("Test Bellman-Ford:\n");
int s = 0;
BellmanFord<Integer> bellmanFord = new BellmanFord<Integer>(g, s);
if( bellmanFord.negativeCycle() )
System.out.println("The graph contain negative cycle!");
else
for( int i = 0 ; i < V ; i ++ ){
if(i == s)
continue;
if(bellmanFord.hasPathTo(i)) {
System.out.println("Shortest Path to " + i + " : " + bellmanFord.shortestPathTo(i));
bellmanFord.showPath(i);
}
else
System.out.println("No Path to " + i );
System.out.println("----------");
}
}
}
对没有负权环图的测试结果testG2.txt:
Test Bellman-Ford:
Shortest Path to 1 : 5.0
0 -> 1
----------
Shortest Path to 2 : 1.0
0 -> 1 -> 2
----------
Shortest Path to 3 : 3.0
0 -> 1 -> 2 -> 4 -> 3
----------
Shortest Path to 4 : 6.0
0 -> 1 -> 2 -> 4
----------
对有负权环图testG_negative_circle.txt的测试结果:
Test Bellman-Ford:
The graph contain negative cycle!