红黑树
红黑树的定义
红黑树是一棵二分搜索树。
红黑树的五个性质:
1、每个结点或者是红的,或者是黑的。
2、根结点是黑的。
3、每一个叶结点(nil结点,即最后的空结点)是黑的。
4、如果一个结点是红的,则其孩子结点都是黑的。
5、对于任意结点,从该结点到其子孙叶结点(nil结点)的所有路径上包含相同数目的黑结点。
红黑树是保持“黑平衡”的二叉树。严格意义上并不是平衡二叉树。因为有红色结点,所以红黑树的最大高度为O(logn)。
与AVL树相比,如果添加和删除操作比较频繁,那么用红黑树将有很大的优势。但是如果使用的数据近乎是不会改变,只涉及到查询操作,那么AVL树比红黑树有优势(虽然它们的查询复杂度都是O(logn))。
2-3树
2-3树满足二分搜索树的基本性质。
结点可以存放一个元素或者两个元素。
在《算法4》中,2-3树的定义如下:
一棵2-3查找树或为一棵空树,或由以下结点组成: 2-结点,含有一个建(与其对应的值)和两条链接,左链接指向的2-3树中的键都小于该结点,右链接指向的2-3树中的键都大于该结点。 3-结点,含有两个键(及其对应的值)和三条链接,左链接指向的2-3树中的键都小于该结点,中链接指向的2-3树中的键都位于该结点的两个键之间,右链接指向的2-3树中的键都大于该结点。
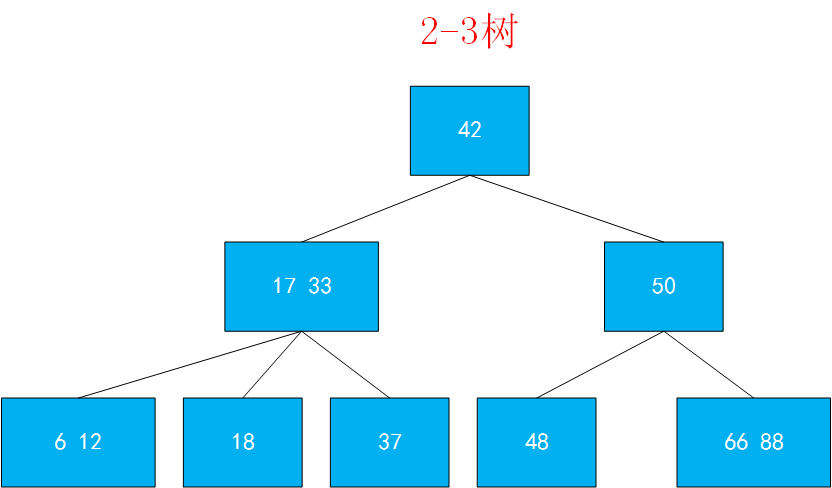
2-3树是一棵绝对平衡的树。
一棵完美平衡的2-3查找树中的所有空链接到根结点的距离都应该是相同的。
2-3树的绝对平衡性
插入新键
要在2-3树中插入一个新结点,我们可以和二叉查找树一样先进行一次未命中的查找,然后把新结点挂在树的底部。但这样的话树就无法保持完美平衡性。我们使用2-3树的蛀牙原因就在于它能够在插入后继续保持平衡。如果未命中的查找结束于一个2-结点,事情就好办了:我们只要把这个2-结点替换为一个3-结点,将要插入的键保存在其中即可。
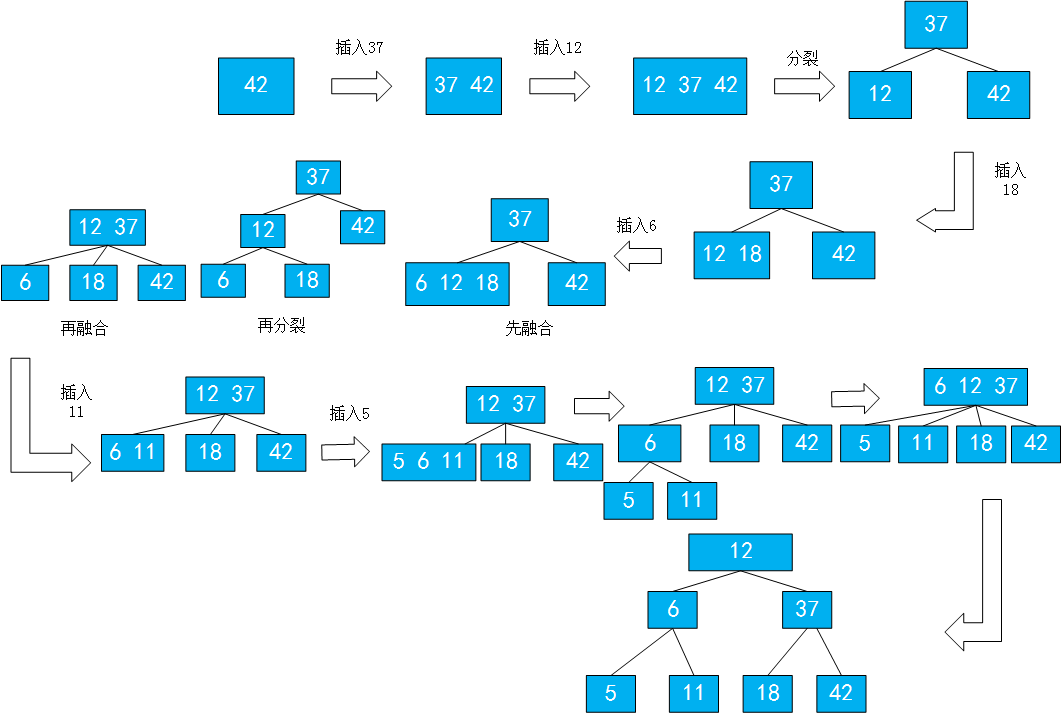
在2-3树中,添加一个结点将永远不会添加到一个空的位置。如图,如果将37插入到以42为根的2-3树中,插入37时,因为42的左孩子为空,新结点将融合到之前添加过程中最后的一个叶子结点上,即42,所以产生了结点融合.42由2-结点变成了3-结点。而若如果继续添加一个12结点,那么由于12小于37,它要添加到3-树的左子树,又因为2-3树的性质,不能添加到空的位置,那么先将12与3-树进行融合,产生一个4-树,接着进行分裂操作。这时候一个4-结点就转变成了一个由3个2-结点组成的平衡的树,同时这棵树保持着绝对平衡。此时,如果继续添加一个18结点,那么18要添加到12的右子树,12的右子树为空,不能添加到空结点,而是与它找到的最后一个叶子结点,即12结点进行融合,从而成为一个3-结点。接着插入6结点,6从根结点出发,比37小,要插入到37的左子树上,而其左子树是12 18的3-结点,它比12要小,所以要插入到其左子树,但它的左子树是一棵空树,添加结点不能添加到一个空的位置,而是找到它最后添加位置的叶子结点,与叶子结点进行融合,此时的叶子结点是一个3-结点,暂时与其融合成为4-结点,然后进行分裂拆解,但是此时如果拆解,那么树将不是一个绝对平衡的二叉树,而是应该将此时拆解后的新的根结点12与其父结点37进行融合,37是一个2-结点,进行融合就很容易了,37融合成3-结点,进而12结点对应的左右孩子变为新的根结点的左孩子和中孩子。继续添加11结点,11应插入到根结点的总左子树,11比6大,本应插入到6的右子树,但是6的右子树为空,所以11和6融合。再插入5,5应插入到12 37的左子树6 11的左结点,其左结点为空,此时应与其融合,首先融合成4-结点,再分裂为3个2-结点,6接着应与父结点融合,形成一个4-结点,4-结点应该进行分裂,分裂成3个2-结点。至此所有结点都是2-结点,仍是平衡的。
其实总结来说添加元素,添加的结点不会添加到空的位置,它会添加到最后搜索到的叶子结点,与其融合。如果其本身是2-结点,那么融合为3-结点,如果本身是3-结点,先融合为4-结点后,在分裂为3个2-结点。
2-3树和红黑树的等价性
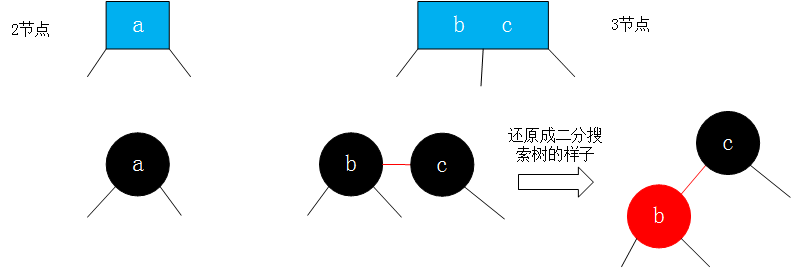
在使用2-3树进行表达和实现时,有的结点包含2个子结点,有的结点包含3个子结点。使用红黑树,均使用含有两个子结点的结点进行表达。
以下是《算法4》中关于替换3-结点的描述:
红黑二叉查找树背后的基本思想是用标准的二叉查找树(完全由2-结点构成)和一些额外的信息(替换3-结点)来表示2-3树。我们将树中的链接分为两种类型:红连接将两个2-结点连接起来构成一个3-结点,黑链接则是2-3树中的普通链接。确切地说,我们将3-结点表示为由一条左斜的红色链接(两个2-结点其中之一是另一个的左子结点)相连的两个2-结点。这种表示法的一个优点是,我们无需修改就可以直接使用标准二叉查找树的get()方法。对于任意的2-3树,只要对结点进行转换,我们都可以立即派生出一棵对应的二叉查找树。我们将这种表示2-3树的二叉查找树称为红黑二叉树(以下简称为红黑树)。
红黑树的另一种定义是含有红黑链接并满足下列条件的二叉查找树: 1.红链接均为左链接 2.没有任何一个结点同时和两条红链接相连 3.该树是完美黑色平衡的,即任意空链接到根结点的路径上的黑链接数量相同 满足这样定义的红黑树和相应的2-3树是一一对应的
即红结点和它的父结点一起表示原来2-3树中的3-结点。所有的红色结点都是向左倾斜的。
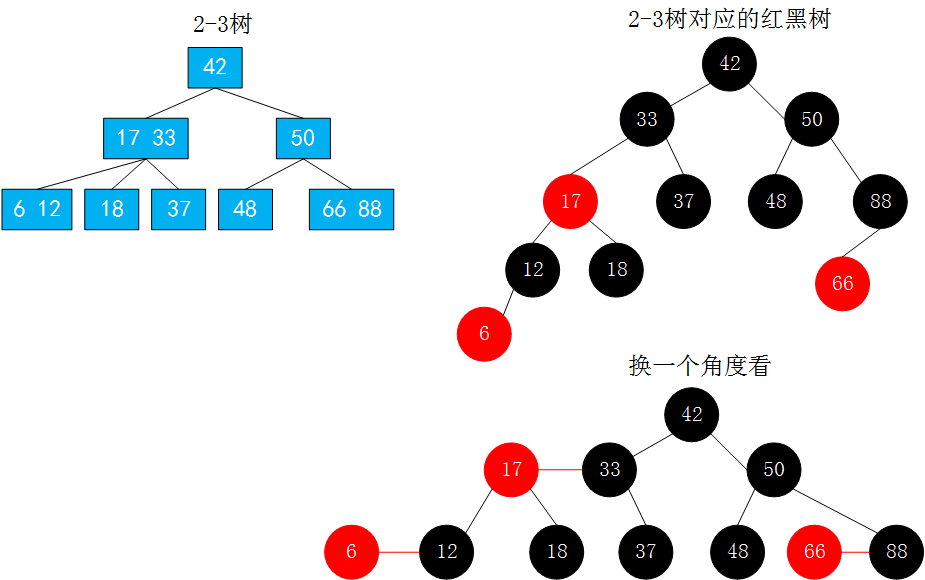
在原来的2-3树中有3个3-结点,所以在红黑树中有3个红结点。
颜色表示
直接上代码吧:
import java.util.ArrayList;
public class RBTree<K extends Comparable<K>,V> {
private static final boolean RED = true;
private static final boolean BLACK = false;
private class Node{
public K key;
public V value;
public Node left,right;
public boolean color;//由其父结点指向它的链接的颜色
public Node(K key,V value){
this.key = key;
this.value = value;
left = null;
right = null;
color = RED; //初始化为红结点,相当于刚创建时就与其父结点进行融合,融合后的操作是后续的事。
}
}
private Node root;
private int size;
public RBTree() {
root = null;
size = 0;
}
// 返回以node为根节点的二分搜索树中,key所在的节点
private Node getNode(Node node, K key){
if(node == null)
return null;
if(key.equals(node.key))
return node;
else if(key.compareTo(node.key) < 0)
return getNode(node.left, key);
else // if(key.compareTo(node.key) > 0)
return getNode(node.right, key);
}
public boolean contains(K key){return getNode(root,key) != null;}
public V get(K key){
Node node = getNode(root,key);
return node == null ? null : node.value;
}
}
在红黑树中添加新元素
在2-3树中添加一个新结点时,它都是或者添加进2-结点,行程一个3-结点;或者是添加进3-结点,暂时形成一个4-结点,然后在进行后续的操作。总之就是把要添加的元素融合到已有的结点中。所以在红黑树中假设永远添加红色结点的意图也就是,添加的结点和其他结点先融合。
在上面的代码中可以看到,我们将新添加的结点定义为红结点。所以在添加时有几种情况。
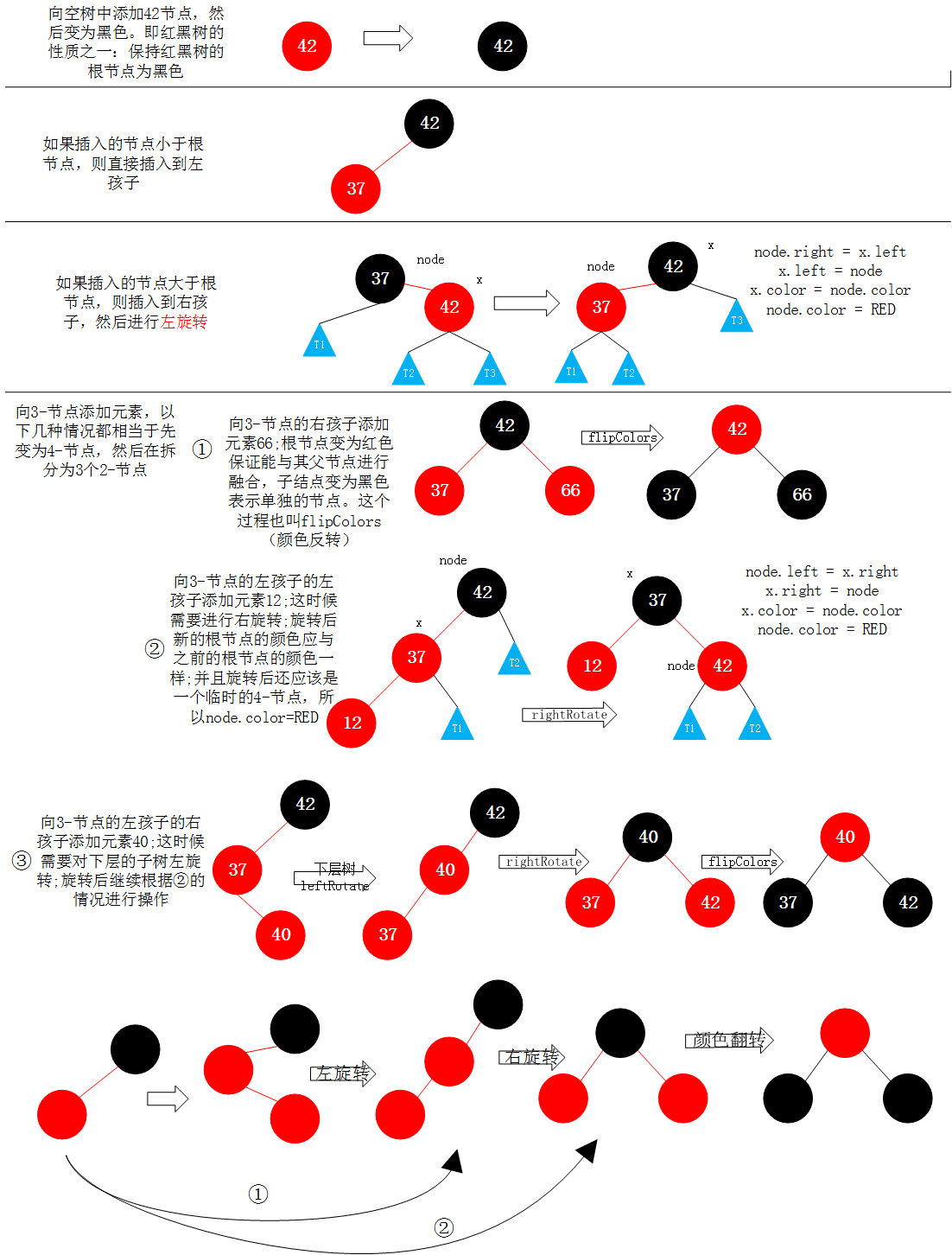
1.最初情况是刚开始的树为空,然后让红黑树的根为新添加的元素,然后让根结点的红色变为黑色。
2.要添加的结点小于根结点,即添加到根结点的左孩子位置,则直接添加过去就可以了。
3.要添加的结点大于根结点,则先添加到根结点的右孩子位置,然后进行左旋转。左旋转方法和AVL树的左旋转类似。在左旋转后,有可能会产生两个红色结点(x.color = node.color;node.color = RED;),这时候不用担心,因为返回的根结点如果为红色,它将会继续和上一层进行相关转换操作。
4.向红黑树中的3-结点添加元素时: ①:向3-结点的右孩子添加时,直接添加到右孩子,然后所有子结点变为黑结点,也就是相当于在2-3树中先将3-结点变为4-结点,然后再分离为3个2-结点,然后再和其上面的父结点进行融合,所以这里要将其根结点变为红色(这样才能保证在红黑树中这个结点和其父结点进行融合) ②:向3-结点添加元素时,新元素小于根结点的左孩子(即新键小于原树中的两个键),需要继续添加到根结点的左孩子的左孩子(即连接到最左边的空链接),它应该是一个红色结点,这样就产生了两个连续的红链接。此时需要将上层的红链接右旋转(中值键作为根结点并和其他两个结点用红链接相连) ③:如果新键的值介于原树中的两个树之间,这样又会产生两个连续的红链接,一条红色左链接一条红色右链接。这时候需要将下层的红链接左旋转得到第②种情况,然后在②情况的基础上继续操作。
维护红黑树的时机和AVL树一样,在基于二分搜索树的基础上,添加了新结点后回溯向上维护。
相关代码:
//判断节点node的颜色
private boolean isRed(Node node){
if(node ==null) {
return BLACK;
}
return node.color;
}
//左旋转
private Node leftRotate(Node node) {
Node x = node.right;
//左旋转操作
node.right = x.left;
x.left = node;
x.color = node.color;
node.color = RED;
return x;
}
//右旋转
private Node rightRotate(Node node) {
Node x = node.left;
//右旋转
node.left = x.right;
x.right = node;
x.color = node.color;
node.color = RED;
return x;
}
//颜色翻转
private void flipColors(Node node){
node.color = RED;
node.left.color = BLACK;
node.right.color = BLACK;
}
//向红黑树中添加新元素(key,value)
public void add(K key,V value){
root = add(root,key,value);
root.color = BLACK;//保证最后的根节点为黑色
}
//向以node为根的红黑树中插入元素(key,value),递归算法
//返回插入新节点后红黑树的根
private Node add(Node node,K key,V value){
if(node == null){
size ++;
return new Node(key,value); //默认插入红色结点
}
if(key.compareTo(node.key) < 0)
node.left = add(node.left,key,value);
else if(key.compareTo(node.key) > 0)
node.right = add(node.right,key,value);
else
node.value = value;
//插入结点结束后,进行红黑树性质的维护
//如果右孩子是红色,左孩子不是红色,则进行左旋转
if(isRed(node.right) && !isRed(node.left))
node = leftRotate(node);
//如果左孩子是红色,左孩子的左孩子也是红色,则进行右旋转
if(isRed(node.left) && isRed(node.left.left))
node = rightRotate(node);
//如果node的左孩子和右孩子都是红结点,则进行颜色反转
if(isRed(node.left) && isRed(node.right))
flipColors(node);
return node;
}
与其他树的比较
如果对于完全随机的数据,普通的二分搜索树BST就已经很好用了。 缺点:极端情况下退化成链表(高度不平衡)
对于查询较多的情况,AVL树的性能很好。 红黑树牺牲了平衡性(2logn的高度)
红黑树的统计性能更优(综合增删改查所有的操作)
红黑树中删除节点
删除节点的操作较为复杂,以后有缘在整理 0.0