AVL
AVL的定义和平衡因子
AVL树即平衡二叉树。AVL树的定义首先要求该树是二叉查找树(满足排序规则),并在此基础上增加了每个节点的平衡因子的定义,一个节点的平衡因子是该节点的左子树树高减去右子树树高的值。 特点:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。在AVL树中任何节点的两个子树的高度最大差别为一,所以它也被称为平衡二叉树
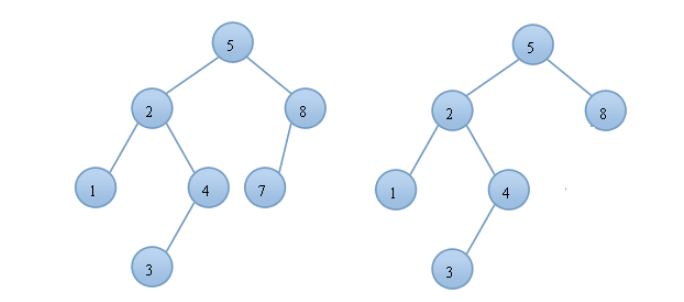
平衡因子BF:该节点的左子树的深度减去它的右子树深度。
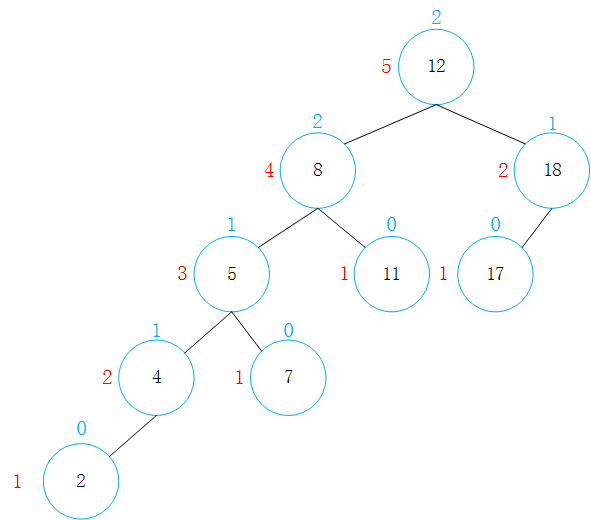
可见图中的平衡因子有2,那么这棵树不是一个平衡二叉树。
计算节点的高度和平衡因子
由上面的定义可以知道,如果想保持二分搜索树的平衡,那么要计算每个节点的高度值,以便计算平衡因子,根据平衡因子对二分搜索树进行一定操作,以便保持平衡。
在之前BST的基础上进行改写(BST见附录),实现新的AVL.
import java.util.ArrayList;
public class BST<K extends Comparable<K>, V> {
private class Node{
public K key;
public V value;
public Node left, right;
public int heigth; //树的高度
public Node(K key, V value){
this.key = key;
this.value = value;
left = null;
right = null;
heigth = 1; //初始化时为1
}
}
//判断该二叉树是否是一棵二分搜索树
//二分搜索树的一个性质之一:在进行中序遍历时,遍历的结果所有元素是按顺序排列的
public boolean isBST(){
ArrayList<K> keys = new ArrayList<>();
inOrder(root,keys);
for(int i = 1 ; i < keys.size() ; i ++){
if(keys.get(i - 1).compareTo(keys.get(i)) > 0)
return false;
}
return true;
}
private void inOrder(Node node,ArrayList<K> keys){
if(node == null)
return;
inOrder(node.left,keys);
keys.add(node.key);
inOrder(node.right,keys);
}
//判断该二叉树是否是一棵平衡二叉树
public boolean isBalanced(){
return isBalanced(root);
}
//判断以Node为根的二叉树是否是一颗平衡二叉树,递归算法
private boolean isBalanced(Node node){
if(node == null)
return true;
int balanceFactor = getBalanceFactor(node);
if(Math.abs(balanceFactor) > 1 )
return false;
return isBalanced(node.left) && isBalanced(node.right);
}
//获得节点node的高度
private int getHeight(Node node){
if(node == null)
return 0;
return node.heigth;
}
//获得节点的平衡因子
private int getBalanceFactor(Node node){
if(node == null)
return 0;
return getHeight(node.left) - getHeight(node.right);
}
// 向以node为根的二分搜索树中插入元素(key, value),递归算法
// 返回插入新节点后二分搜索树的根
//在这个函数中要对height进行维护
private Node add(Node node, K key, V value){
if(node == null){
size ++;
return new Node(key, value);
}
if(key.compareTo(node.key) < 0)
node.left = add(node.left, key, value);
else if(key.compareTo(node.key) > 0)
node.right = add(node.right, key, value);
else // key.compareTo(node.key) == 0
node.value = value;
// 更新height
node.heigth = 1 + Math.max(getHeight(node.left),getHeight(node.right));
//计算平衡因子
int balanceFactor = getBalanceFactor(node);
if(Math.abs(balanceFactor) > 1)
System.out.println("unbalanced :" + balanceFactor);
return node;
}
}
以上代码对AVL树的基本操作进行了编写,其中省略了部分和BST相同的代码
旋转操作
在进行了插入节点的操作后,才有可能破坏当前树的平衡性。这时候需要重新计算其父节点和祖先节点的平衡因子,并判断是否失去了平衡性。因为本身插入节点的add操作就是用递归实现的,所以在递归代码中进行改写。
右旋转
如果平衡因子大于一并且是在树的左侧的左侧添加
如图所示,是两种最简单的向左添加破坏了树的平衡性的情况,以绿色表示的节点其整体向左倾斜.左子树的高度大于其右子树的高度并且其左孩子也是如此。
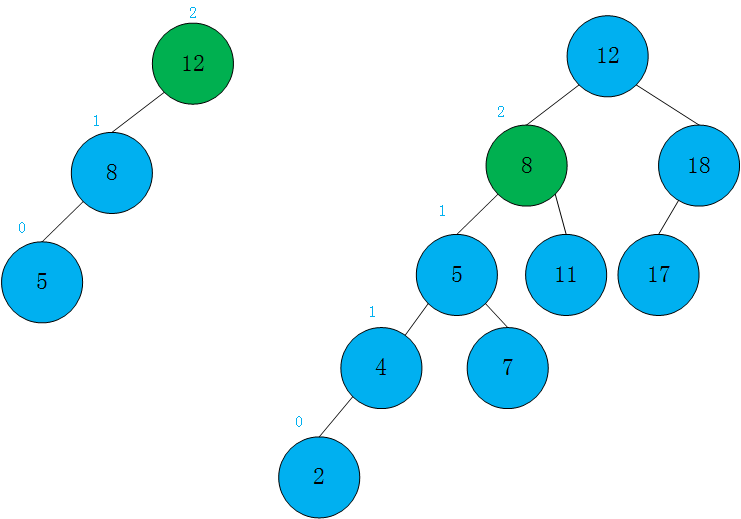
这时候的解决方法是进行右旋转。
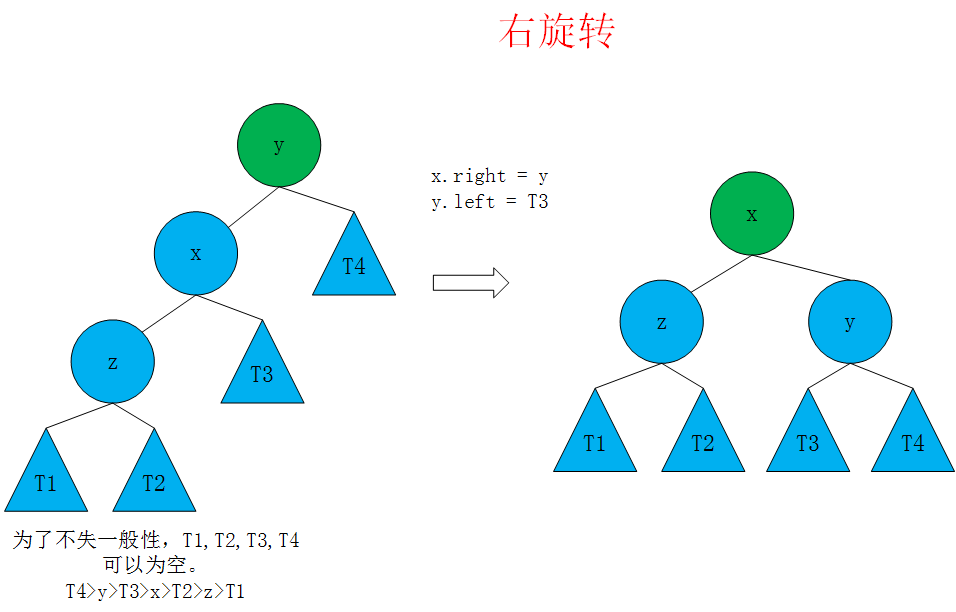
在add函数中进行修改:
//对节点y进行向右旋转操作,返回旋转后的新的根节点x
// y x
// / \ / \
// x T4 向右旋转 (y) z y
// / \ - - - - - - - -> / \ / \
// z T3 T1 T2 T3 T4
// / \
// T1 T2
private Node rightRotate(Node y){
Node x = y.left;
Node T3 = x.right;
//向右旋转
x.right = y;
y.left = T3;
//更新height
y.heigth = Math.max(getHeight(y.left),getHeight(y.right));
x.heigth = Math.max(getHeight(x.left),getHeight(x.right));
return x;
}
private Node add(Node node, K key, V value){
if(node == null){
size ++;
return new Node(key, value);
}
if(key.compareTo(node.key) < 0)
node.left = add(node.left, key, value);
else if(key.compareTo(node.key) > 0)
node.right = add(node.right, key, value);
else // key.compareTo(node.key) == 0
node.value = value;
// 更新height
node.heigth = 1 + Math.max(getHeight(node.left),getHeight(node.right));
//计算平衡因子
int balanceFactor = getBalanceFactor(node);
// if(Math.abs(balanceFactor) > 1)
// System.out.println("unbalanced :" + balanceFactor);
///平衡维护
if(balanceFactor > 1 && getBalanceFactor(node.left) >= 0)
return rightRotate(node);
return node;
}
左旋转
同理,当插入的元素在不平衡的节点的右侧的右侧时,进行坐旋转操作以满足平衡性。即左旋转的情况是和右旋转完全对称的。
// 对节点y进行向左旋转操作,返回旋转后新的根节点x
// y x
// / \ / \
// T1 x 向左旋转 (y) y z
// / \ - - - - - - - -> / \ / \
// T2 z T1 T2 T3 T4
// / \
// T3 T4
private Node leftRotate(Node y){
Node x = y.right;
Node T2 = x.left;
//向左旋转
x.left = y;
y.right = T2;
//更新height
y.heigth = Math.max(getHeight(y.left),getHeight(y.right)) + 1;
x.heigth = Math.max(getHeight(x.left),getHeight(x.right)) + 1;
return x;
}
private Node add(Node node, K key, V value){
//...省略部分代码
//平衡维护
if(balanceFactor > 1 && getBalanceFactor(node.left) >= 0) //左子树比右子树高
return rightRotate(node);
if(balanceFactor < -1 && getBalanceFactor(node.right) <= 0) //右子树比左子树高
return leftRotate(node);
return node;
}
LR和RL
LR
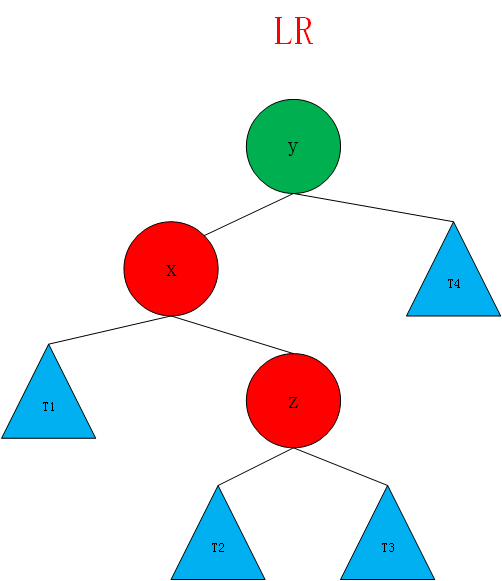
当插入的元素在不平衡节点的左侧的右侧(即LR),这时候不能仅仅使用右旋转。 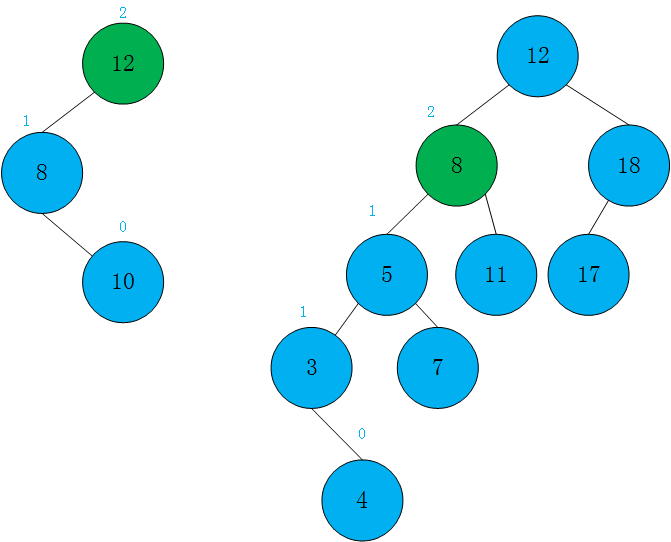
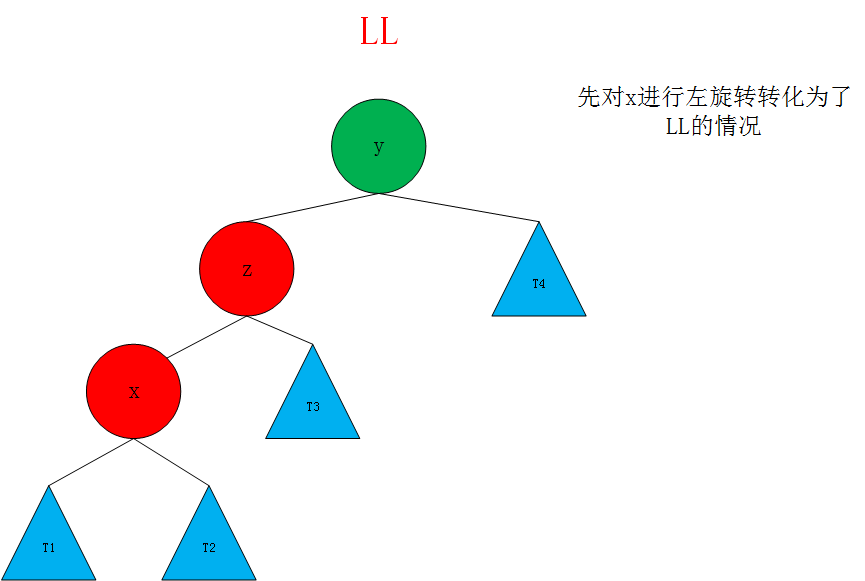
这时候需要先对x进行左旋转,转化为LL的情况
到了这种情况继续对y进行右旋转就可以了。 继续完善平衡维护的代码:
//..省略代码
//平衡维护
// LL
if(balanceFactor > 1 && getBalanceFactor(node.left) >= 0) //左子树比右子树高
return rightRotate(node);
// RR
if(balanceFactor < -1 && getBalanceFactor(node.right) <= 0) //右子树比左子树高
return leftRotate(node);
// LR
if(balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
node.left = leftRotate(node.left); //转换为LL
return rightRotate(node);
}
//..省略代码
RL
RL是LR对称的一种情况,先将其转化为RR的情况,在进行左旋转。就不在赘述了。
// RL
if(balanceFactor < -1 && getBalanceFactor(node.right) > 0) {
node.right = rightRotate(node.right); //转化为RR
return leftRotate(node);
}
删除元素
删除元素也和添加元素类似,在删除元素后有可能会破坏原树的平衡性,所以在删除元素后要进行向上递归的操作,逐层判断,调整树的平衡。
在平衡二叉树的删除操作中,node.left或者node.right接到了递归操作的新的node节点后,当前的node节点的平衡性有可能已经遭到了破坏,所以不能直接返回当前的node,要先维护node的平衡,不能这么早的return node;,所以先用retNode暂存一下要返回的node.这样就有机会对retNode进行平衡维护,然后再返回。同理, key.compareTo(node.key) == 0时,待删除节点左子树或者右子树为空时返回的node也暂时赋值给retNode.同样待删除节点左右子树均不为空的情况也是用retNode暂存。
这样,retNode中存储的就是删除了节点后要返回的新的node.所以在得到了retNode后要对retNode进行判断,然后维护平衡。这时候的维护平衡操作其实和添加是一样的,先更新height,然后计算平衡因子,最后根据不同情况进行旋转。只是这时候处理的对象是retNode。
要注意在removeMin(Node node)函数操作时也有可能打破平衡,所以也要在这个函数中进行平衡维护。其实可以改写为successor.right = remove(node.right,successor.key);因为remove()函数添加了对平衡性的处理,所以这里的删除最小值操作这样改写是可以的。
// 从二分搜索树中删除键为key的节点
public V remove(K key){
Node node = getNode(root, key);
if(node != null){
root = remove(root, key);
return node.value;
}
return null;
}
private Node remove(Node node, K key){
if( node == null )
return null;
Node retNode;
if( key.compareTo(node.key) < 0 ){
node.left = remove(node.left , key);
retNode = node;
}
else if(key.compareTo(node.key) > 0 ){
node.right = remove(node.right, key);
retNode = node;
}
else{ // key.compareTo(node.key) == 0
// 待删除节点左子树为空的情况
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
retNode = rightNode;
}
// 待删除节点右子树为空的情况
else if(node.right == null){
Node leftNode = node.left;
node.left = null;
size --;
retNode = leftNode;
}
else {// 待删除节点左右子树均不为空的情况
// 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
// 用这个节点顶替待删除节点的位置
Node successor = minimum(node.right);
successor.right = remove(node.right, successor.key);
successor.left = node.left;
node.left = node.right = null;
retNode = successor;
}
}
//判断为空的情况,以免访问height会出错
if(retNode == null)
return null;
//更新height
retNode.heigth = 1 + Math.max(getHeight(retNode.left),getHeight(retNode.right));
//计算平衡因子
int balanceFactor = getBalanceFactor(retNode);
//平衡维护
// LL
if(balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0) //左子树比右子树高
return rightRotate(retNode);
// RR
if(balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0) //右子树比左子树高
return leftRotate(retNode);
// LR
if(balanceFactor > 1 && getBalanceFactor(retNode.left) < 0) {
retNode.left = leftRotate(retNode.left); //转换为LL
return rightRotate(retNode);
}
// RL
if(balanceFactor < -1 && getBalanceFactor(retNode.right) > 0) {
retNode.right = rightRotate(retNode.right); //转化为RR
return leftRotate(retNode);
}
return retNode;
}
基于AVL树的set和map
Map
public interface Map<K,V> {
void add(K key,V value);
V remove(K key); //删除key对应的键值对,并返回值
boolean contains(K key); //是否存已在key
V get(K key); //获得key对应的value值
void set(K key,V newValue); //更新值
int getSize();
boolean isEmpty();
}
public class AVLMap<K extends Comparable<K>,V> implements Map<K,V> {
private AVLTree<K,V> avl;
public AVLMap(){
avl = new AVLTree<>();
}
@Override
public int getSize(){
return avl.getSize();
}
@Override
public boolean isEmpty(){
return avl.isEmpty();
}
@Override
public void add(K key,V value){
avl.add(key,value);
}
@Override
public boolean contains(K key){
return avl.contains(key);
}
@Override
public V get(K key){
return avl.get(key);
}
@Override
public void set(K key,V newValue){
avl.set(key,newValue);
}
@Override
public V remove(K key){
return avl.remove(key);
}
}
Set
public interface Set<E> {
void add(E e);
void remove(E e);
boolean isEmpty();
boolean containes(E e);
int getSize();
}
public class AVLSet<E extends Comparable<E>> implements Set<E> {
private AVLTree<E, Object> avl;
public AVLSet(){
avl = new AVLTree<>();
}
@Override
public int getSize(){
return avl.getSize();
}
@Override
public boolean isEmpty(){
return avl.isEmpty();
}
@Override
public boolean containes(E e) {
return avl.contains(e);
}
@Override
public void add(E e){
avl.add(e, null);
}
@Override
public void remove(E e){
avl.remove(e);
}
}
附录
BST
import java.util.ArrayList;
public class BST<K extends Comparable<K>, V> {
private class Node{
public K key;
public V value;
public Node left, right;
public Node(K key, V value){
this.key = key;
this.value = value;
left = null;
right = null;
}
}
private Node root;
private int size;
public BST(){
root = null;
size = 0;
}
public int getSize(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
// 向二分搜索树中添加新的元素(key, value)
public void add(K key, V value){
root = add(root, key, value);
}
// 向以node为根的二分搜索树中插入元素(key, value),递归算法
// 返回插入新节点后二分搜索树的根
private Node add(Node node, K key, V value){
if(node == null){
size ++;
return new Node(key, value);
}
if(key.compareTo(node.key) < 0)
node.left = add(node.left, key, value);
else if(key.compareTo(node.key) > 0)
node.right = add(node.right, key, value);
else // key.compareTo(node.key) == 0
node.value = value;
return node;
}
// 返回以node为根节点的二分搜索树中,key所在的节点
private Node getNode(Node node, K key){
if(node == null)
return null;
if(key.equals(node.key))
return node;
else if(key.compareTo(node.key) < 0)
return getNode(node.left, key);
else // if(key.compareTo(node.key) > 0)
return getNode(node.right, key);
}
public boolean contains(K key){
return getNode(root, key) != null;
}
public V get(K key){
Node node = getNode(root, key);
return node == null ? null : node.value;
}
public void set(K key, V newValue){
Node node = getNode(root, key);
if(node == null)
throw new IllegalArgumentException(key + " doesn't exist!");
node.value = newValue;
}
// 返回以node为根的二分搜索树的最小值所在的节点
private Node minimum(Node node){
if(node.left == null)
return node;
return minimum(node.left);
}
// 删除掉以node为根的二分搜索树中的最小节点
// 返回删除节点后新的二分搜索树的根
private Node removeMin(Node node){
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
// 从二分搜索树中删除键为key的节点
public V remove(K key){
Node node = getNode(root, key);
if(node != null){
root = remove(root, key);
return node.value;
}
return null;
}
private Node remove(Node node, K key){
if( node == null )
return null;
if( key.compareTo(node.key) < 0 ){
node.left = remove(node.left , key);
return node;
}
else if(key.compareTo(node.key) > 0 ){
node.right = remove(node.right, key);
return node;
}
else{ // key.compareTo(node.key) == 0
// 待删除节点左子树为空的情况
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
// 待删除节点右子树为空的情况
if(node.right == null){
Node leftNode = node.left;
node.left = null;
size --;
return leftNode;
}
// 待删除节点左右子树均不为空的情况
// 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
// 用这个节点顶替待删除节点的位置
Node successor = minimum(node.right);
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
return successor;
}
}
public static void main(String[] args){
System.out.println("sorcerers.stone.txt");
ArrayList<String> words = new ArrayList<>();
if(FileOperation.readFile("sorcerers.stone.txt", words)) {
System.out.println("Total words: " + words.size());
BST<String, Integer> map = new BST<>();
for (String word : words) {
if (map.contains(word))
map.set(word, map.get(word) + 1);
else
map.add(word, 1);
}
System.out.println("Total different words: " + map.getSize());
System.out.println("Frequency of go: " + map.get("go"));
System.out.println("Frequency of stone: " + map.get("stone"));
}
System.out.println();
}
}